TransformationFunction[data]
represents a transformation function that applies geometric and other transformations.


TransformationFunction
TransformationFunction[data]
represents a transformation function that applies geometric and other transformations.
Details


- TransformationFunction[…] objects are generated by constructors such as TranslationTransform, RotationTransform, etc.
- TransformationFunction[…][x] applies the transformation function to a vector x, returning a transformed vector.
- TransformationFunction[…][{x1,x2,…}] for a list of vectors applies the transformation to each vector xi, producing a list of transformed vectors.
- TransformationFunction works with both numerical and symbolic vectors and represents a linear fractional transformation
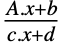 , where A∈Matrices[{m,n}], b∈Matrices[{m,1}], c∈Matrices[{1,n}] and d∈Matrices[{1,1}].
, where A∈Matrices[{m,n}], b∈Matrices[{m,1}], c∈Matrices[{1,n}] and d∈Matrices[{1,1}]. - For smaller dimensions, it is typically displayed as an
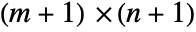 transformation matrix
transformation matrix 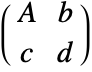 . TransformationMatrix can be used to extract the transformation matrix.
. TransformationMatrix can be used to extract the transformation matrix. - Composition[t1,t2] where ti has transformation matrix
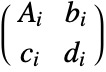 gives a new TransformationFunction object with transformation matrix
gives a new TransformationFunction object with transformation matrix 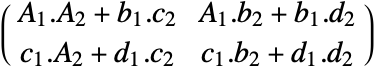 .
. - InverseFunction[t] where t has transformation matrix
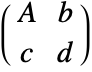 gives a new TransformationFunction object with transformation matrix
gives a new TransformationFunction object with transformation matrix 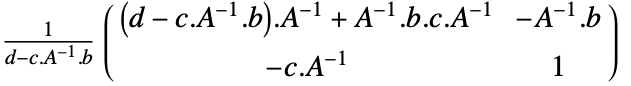 where
where 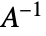 is the matrix inverse.
is the matrix inverse. - GeometricTransformation can be used to represent the effect of applying a TransformationFunction object to geometrical or graphics objects when restricted to affine transformations.
- TransformationFunction[…][prop] gives the transformation property prop. For a transformation function with transformation matrix
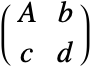 , properties include:
, properties include: -
"AffineQ" whether the transformation is structurally affine or not, it gives True if both c and d are zero "AffineMatrix" the matrix A "AffineVector" the vector b "FractionalVector" the vector c "FractionalConstant" the constant d "ArgumentLength" the length n of the vector x "ResultLength" the length m of the result vector "TransformationMatrix" 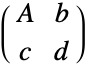
Examples
open all close allScope (15)
Constructing TransformationFunction (10)
A translation by the vector {qx,qy,qz}:
Scaling along the coordinate axes:
Shearing in the ![]() direction by an angle θ:
direction by an angle θ:
Rescaling the box [xmin, xmax][ymin, ymax] to the unit square:
A general TransformationFunction:
Working with TransformationFunction as a Function (4)
Applications (2)
TransformationFunction can be used as an argument to GeometricTransformation:
Integrate a function over a rhombic region:
![]() defines a change of variables that maps the unit square to the integration region:
defines a change of variables that maps the unit square to the integration region:
Properties & Relations (1)
Find the ![]()
![]() power of a transformation:
power of a transformation:
Find the ![]()
![]() iteration using RSolve:
iteration using RSolve:
Related Guides
Text
Wolfram Research (2007), TransformationFunction, Wolfram Language function, https://reference.wolfram.com/language/ref/TransformationFunction.html (updated 2019).
CMS
Wolfram Language. 2007. "TransformationFunction." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/TransformationFunction.html.
APA
Wolfram Language. (2007). TransformationFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TransformationFunction.html
BibTeX
@misc{reference.wolfram_2025_transformationfunction, author="Wolfram Research", title="{TransformationFunction}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/TransformationFunction.html}", note=[Accessed: 11-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_transformationfunction, organization={Wolfram Research}, title={TransformationFunction}, year={2019}, url={https://reference.wolfram.com/language/ref/TransformationFunction.html}, note=[Accessed: 11-January-2026]}