WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

TransformationFunction[data]

幾何学的変換およびその他の変換を適用する変換関数を表す．

詳細
Details and Options Details and Options
例題  
例  
スコープ  
TransformationFunctionの構築  
TransformationFunctionを関数として使う  
TransformationFunctionを公式として使う  
アプリケーション  
特性と関係  
関連項目
関連するガイド
履歴
引用書式

TransformationFunction

TransformationFunction[data]

幾何学的変換およびその他の変換を適用する変換関数を表す．

詳細

  • TransformationFunction[…]オブジェクトは，TranslationTransformやRotationTransform等のコンストラクタによって生成される．
  • TransformationFunction[…][x]は，変換関数をベクトル x に適用し，変換されたベクトルを返す．
  • ベクトルのリストについてのTransformationFunction[…][{x1,x2,…}]は，変換を各ベクトル xiに適用し，変換されたベクトルのリストを生成する．
  • TransformationFunctionは数値ベクトルと記号ベクトルの両方に使うことができ，A∈Matrices[{m,n}]，b∈Matrices[{m,1}]，c∈Matrices[{1,n}]，d∈Matrices[{1,1}]のとき線形分数変換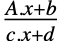を表す．
  • 低次元については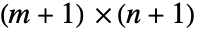，変換行列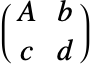として表示される．TransformationMatrixを使って変換行列を抽出することができる．
  • tiが変換行列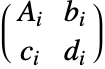を持つComposition[t1,t2]は，変換行列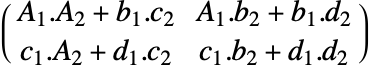を持つ新たなTransformationFunctionオブジェクトを与える．
  • t が変換行列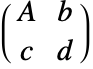を持つInverseFunction[t]は，変換行列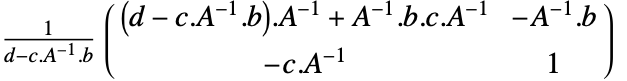を持つ新たなTransformationFunctionオブジェクトを与える．ただし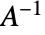，は逆行列である．
  • GeometricTransformationは，アフィン変換に限定されている場合に，TransformationFunctionオブジェクトを幾何学オブジェクトあるいはグラフィックスオブジェクトに適用した結果を表すのに用いることができる．
  • TransformationFunction[…][prop]は，変換特性 prop を与える．次は，変換行列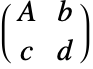特性を含む変換関数である．
  • "AffineQ"変換が構造的にアフィン変換かどうか．c と d の両方が0のときにはTrueを与える．
    "AffineMatrix"行列 A
    "AffineVector"ベクトル b
    "FractionalVector"ベクトル c
    "FractionalConstant"定数 d
    "ArgumentLength"ベクトル x の長さ n
    "ResultLength"結果のベクトルの長さ m
    "TransformationMatrix"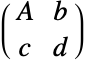

例題

すべて開く すべて閉じる

例  (1)

回転移動を行う：

Wolfram Language code: r = RotationTransform[θ]

これは，ベクトル{x,y}を角 θ 分回転させる：

Wolfram Language code: r[{x, y}]

スコープ  (15)

TransformationFunctionの構築  (10)

ベクトル{qx,qy,qz}分の変換：

Wolfram Language code: t = TranslationTransform[{qx, qy, qz}]
Wolfram Language code: t[{x, y, z}]

軸の周りでの回転：

Wolfram Language code: r = RotationTransform[θ, {0, 0, 1}]
Wolfram Language code: r[{x, y, z}]

座標軸に沿ったスケーリング：

Wolfram Language code: ScalingTransform[{sx, sy}]

方向へ角 θ 分ずらす：

Wolfram Language code: ShearingTransform[θ, {1, 0}, {0, 1}]

平面に写像する：

Wolfram Language code: ReflectionTransform[{0, 0, 1}]

ボックス[xmin, xmax][ymin, ymax]を単位正方形にスケールし直す：

Wolfram Language code: RescalingTransform[{{xmin, xmax}, {ymin, ymax}}]

一般的なTransformationFunction：

Wolfram Language code: t = LinearFractionalTransform[{{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}]
Wolfram Language code: t[{x, y}]

線形変換：

Wolfram Language code: tl = LinearFractionalTransform[{ Array[Subscript[a, #1, #2]&, {2, 2}] }]
Wolfram Language code: tl[{x, y}]

アフィン変換：

Wolfram Language code: ta = LinearFractionalTransform[{ Array[Subscript[a, #1, #2]&, {2, 2}], Array[Subscript[b, #]&, {2}] }]
Wolfram Language code: ta[{x, y}]

一次分数変換：

Wolfram Language code: tlft = LinearFractionalTransform[{Array[Subscript[a, #1, #2]&, {2, 2}], Array[Subscript[b, #]&, {2}], Array[Subscript[c, #]&, {2}]}]
Wolfram Language code: tlft[{x, y}]

TransformationFunctionを関数として使う  (4)

ここでは， は 軸の周りの の回転である：

Wolfram Language code: t = RotationTransform[π / 3., {0, 0, 1}]

これは 軸を変換する：

Wolfram Language code: t[{1, 0, 0}]

これはベクトルのリストを変換する：

Wolfram Language code: vl = RandomReal[1, {10, 3}];
Wolfram Language code: t[vl]

2つの変換を構成する：

Wolfram Language code: t1 = RotationTransform[θ]
Wolfram Language code: t2 = RotationTransform[ϕ]
Wolfram Language code: Composition[t1, t2]//Simplify

逆変換を計算する：

Wolfram Language code: t = RotationTransform[θ]
Wolfram Language code: it = InverseFunction[t]//Simplify

次はこれらが逆変換であることを示している：

Wolfram Language code: Composition[it, t]//Simplify

偏微分を計算する：

Wolfram Language code: f = TransformationFunction[{{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}]
Wolfram Language code: Derivative[{1, 2}][f]

TransformationFunctionを公式として使う  (1)

これは一般的な変換を定義する：

Wolfram Language code: t = LinearFractionalTransform[{ {{1, 2}, {3, 4}}, {1, 2}, {3, 1} }]

これは，対応する公式である：

Wolfram Language code: f = t[{x, y}]

導関数：

Wolfram Language code: D[f, {x, 2}]

極限：

Wolfram Language code: Limit[f, x -> 1]

積分：

Wolfram Language code: Integrate[f, x]

プロット：

Wolfram Language code: Plot3D[f, {x, -1, 1}, {y, -1, 1}, PlotStyle -> {Red, Green}, Exclusions -> {1 + 3x + y == 0}]

アプリケーション  (2)

TransformationFunctionはGeometricTransformationの引数として使うことができる：

Wolfram Language code: t = AffineTransform[{DiagonalMatrix[{2, 2, 1}], {1, 1, 1}}]
Wolfram Language code: Graphics3D[GeometricTransformation[Cylinder[], t], Axes -> True]

菱形の範囲の上で関数を積分する：

Wolfram Language code: Integrate[(x ^ 3 + y ^ 3)Boole[x / 2 < y < x / 2 + 3 / 4 && y / 2 < x < y / 2 + 3 / 4], {x, 0, 3 / 2}, {y, 0, 3 / 2}]

は単位正方形を積分範囲にマップする変数の変化を定義する：

Wolfram Language code: t = AffineTransform[{{1, 1 / 2}, {1 / 2, 1}}]

新たな座標における被積分関数：

Wolfram Language code: fuv = x ^ 3 + y ^ 3 /. Thread[{x, y} -> t[{u, v}]]

ヤコビアン：

Wolfram Language code: jac = Det[TransformationMatrix[t]]
Wolfram Language code: Integrate[fuv Abs[jac], {u, 0, 1}, {v, 0, 1}]

特性と関係  (1)

変換の 次ベキを求める：

Wolfram Language code: t = LinearFractionalTransform[{{-3, 2, 1}, {0, 1, 1}, {4, -2, -4}}]
Wolfram Language code: tt[n_] := LinearFractionalTransform[MatrixPower[TransformationMatrix[t], n]]

tを5回適用する：

Wolfram Language code: Nest[Together@t@#&, {x0, y0}, 5]

tt[5]を適用する：

Wolfram Language code: tt[5][{x0, y0}]
Wolfram Language code: % == %%//Simplify

RSolveを使った 次反復を求める：

Wolfram Language code: RSolve[Thread /@ {{x[n + 1], y[n + 1]} == t[{x[n], y[n]}], {x[0], y[0]} == {x0, y0}}, {x, y}, n]
Wolfram Language code: {x[5], y[5]} /. %[[1]]//Simplify
Wolfram Research (2007), TransformationFunction, Wolfram言語関数， https://reference.wolfram.com/language/ref/TransformationFunction.html （2019年に更新）.

テキスト

Wolfram Research (2007), TransformationFunction, Wolfram言語関数， https://reference.wolfram.com/language/ref/TransformationFunction.html （2019年に更新）.

CMS

Wolfram Language. 2007. "TransformationFunction." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/TransformationFunction.html.

APA

Wolfram Language. (2007). TransformationFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TransformationFunction.html

BibTeX

@misc{reference.wolfram_2026_transformationfunction, author="Wolfram Research", title="{TransformationFunction}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/TransformationFunction.html}", note=[Accessed: 03-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_transformationfunction, organization={Wolfram Research}, title={TransformationFunction}, year={2019}, url={https://reference.wolfram.com/language/ref/TransformationFunction.html}, note=[Accessed: 03-November-2026]}