TruncateSum
TruncateSum[sexpr,n]
truncates each Sum in sexpr to have at most n terms.
TruncateSum[sexpr,{m,n,…}]
truncates each multiple Sum in sexpr using the iterative specification {m,n,…}.
Details and Options

- TruncateSum is typically used to truncate symbolic solutions involving infinite sums to finite sums, making it easy to numerically evaluate such approximations.
- The sum expression sexpr can have any combination of unevaluated and Inactive sums.
- TruncateSum will truncate large positive or negative summation limits according to the following:
-
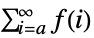
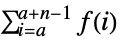
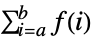
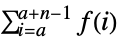 , if
, if 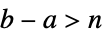
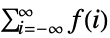
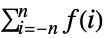
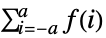
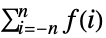 , if
, if 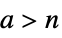
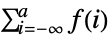
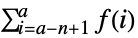
- The following options can be given:
-
ActivateResult True whether to Activate the result WorkingPrecision Automatic the precision used in internal computations
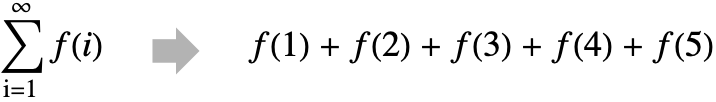
Examples
open allclose allBasic Examples (2)
Scope (13)
Basic Uses (3)
Truncate an infinite sum to its first 10 terms:
Truncate an infinite sum to a sum with a symbolic upper limit:
For unevaluated sums, TruncateSum directly evaluates the truncated sum:
Finite Sums (3)
Infinite Sums (4)
Multiple Sums (2)
Inactive Sums (1)
For inactive sums, TruncateSum tries to evaluate the truncated sum:
Use ActivateResultFalse to avoid activating the inactive sum:
Options (1)
Applications (10)
Differential Equations (4)
Solve the Dirichlet problem for the wave equation on a finite interval:
The solution is an infinite trigonometric series:
Extract the first three terms from the Inactive sum:
Solve the Dirichlet problem for the wave equation in a rectangle:
The solution is a doubly infinite trigonometric series:
Extract a few terms from the Inactive sums:
Solve the Dirichlet problem for the heat equation on a finite interval:
The solution is a Fourier sine series:
Truncate the Inactive sum:
Solve the initial value problem for a Schrödinger equation with Dirichlet boundary conditions:
Define a family of partial sums of the solution:
For each k, uk satisfies the differential equation:
The boundary conditions are also satisfied:
The initial condition is only satisfied for u∞, but there is rapid convergence at t==2:
Asymptotics (3)
Compute the power series expansion of ![]() around 0:
around 0:
Obtain the first seven nonzero terms in the series:
Compute the power series expansion of ![]() around 1:
around 1:
Obtain the first five terms in the series:
Truncate the series for the Hypergeometric1F1 function:
Compare the results with the built-in Hypergeometric1F1 function:
Properties & Relations (4)
TruncateSum[expr,n] truncates each sum in the expression to have at most n terms:
TruncateSum truncates both limits of doubly infinite sums:
TruncateSum truncates only the lower limit of a sum from –∞ to a finite value:
TruncateSum activates all inactive sums in the expression:
Text
Wolfram Research (2024), TruncateSum, Wolfram Language function, https://reference.wolfram.com/language/ref/TruncateSum.html.
CMS
Wolfram Language. 2024. "TruncateSum." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/TruncateSum.html.
APA
Wolfram Language. (2024). TruncateSum. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TruncateSum.html