TruncateSum
TruncateSum[sexpr,n]
对 sexpr 中的 Sum 进行截断,最多包含 n 项.
TruncateSum[sexpr,{m,n,…}]
对 sexpr 中的多个 Sum 进行截断,使用迭代指定 {m,n,…}.
更多信息和选项

- TruncateSum 通常用于将涉及无限和的符号解截断为有限和,从而可以轻松地对此类近似进行数值计算.
- 和表达式 sexpr 可由未计算的和与 Inactive 和进行任意组合而形成.
- TruncateSum 将根据以下条件对大型正的或负的求和极限进行截断:
-
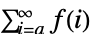
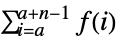
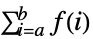
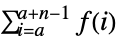 , if
, if 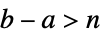
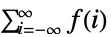
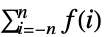
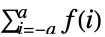
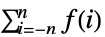 , if
, if 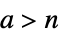
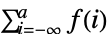
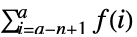
- 可给出以下选项:
-
ActivateResult True 是否 Activate 结果 WorkingPrecision Automatic 内部计算使用的精度
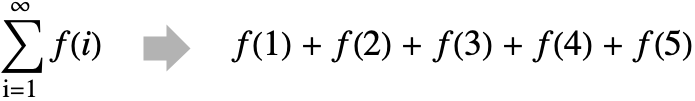
范例
打开所有单元关闭所有单元范围 (13)
基本用法 (3)
处于未激活状态的和 (1)
应用 (10)
微分方程 (4)
渐近 (3)
截断 Hypergeometric1F1 函数的级数:
与内置的 Hypergeometric1F1 函数相比较:
属性和关系 (4)
TruncateSum[expr,n] 将表达式中的每个和截断为最多包含 n 项:
TruncateSum 截断双无限和的两个极限:
TruncateSum 只将和的下限从 –∞ 截断为有限值:
TruncateSum 激活表达式中所有处于未激活状态的和:
Wolfram Research (2024),TruncateSum,Wolfram 语言函数,https://reference.wolfram.com/language/ref/TruncateSum.html.
文本
Wolfram Research (2024),TruncateSum,Wolfram 语言函数,https://reference.wolfram.com/language/ref/TruncateSum.html.
CMS
Wolfram 语言. 2024. "TruncateSum." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/TruncateSum.html.
APA
Wolfram 语言. (2024). TruncateSum. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/TruncateSum.html 年