UnilateralConvolve[f,g,u,t]
gives the unilateral convolution with respect to u of the expressions f and g.
UnilateralConvolve[f,g,{u1,…,un},{t1,…,tn}]
gives the multidimensional unilateral convolution.


UnilateralConvolve
UnilateralConvolve[f,g,u,t]
gives the unilateral convolution with respect to u of the expressions f and g.
UnilateralConvolve[f,g,{u1,…,un},{t1,…,tn}]
gives the multidimensional unilateral convolution.
Details and Options

- UnilateralConvolve is also known as causal convolution.
- The concept of unilateral convolution arises naturally when examining causal systems. The output of such systems at any time depends only on values of the input at the present time and in the past.
- The unilateral convolution
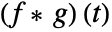 of two functions
of two functions 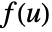 and
and 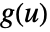 is given by
is given by 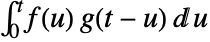 .
. - The lower limit of the integral is effectively taken to be
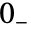 , so that
, so that 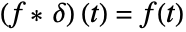 where
where ![TemplateBox[{{t}}, DiracDeltaSeq] TemplateBox[{{t}}, DiracDeltaSeq]](Files/UnilateralConvolve.en/7.png) is the DiracDelta function.
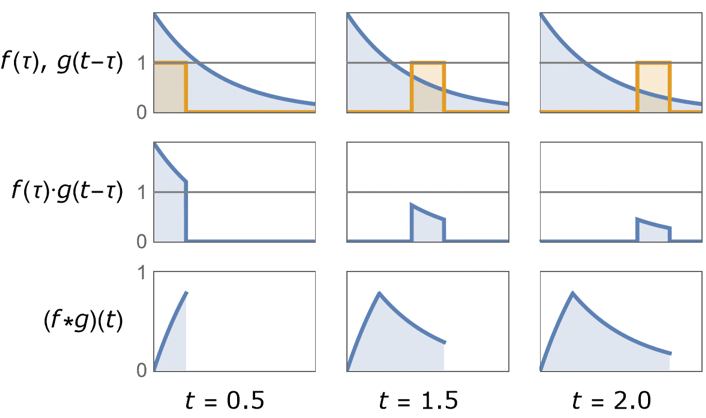
is the DiracDelta function. - The following demonstrates the unilateral convolution of exponential and unit box functions.
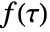 represents an exponential function and
represents an exponential function and 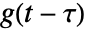 represents the reflected and shifted unit box function. The convolution
represents the reflected and shifted unit box function. The convolution 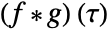 is the area under the product
is the area under the product 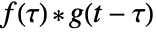 from
from  to
to  .
. - The multidimensional convolution is given by
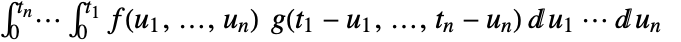 .
. - The following options can be given:
-
Assumptions $Assumptions assumptions to make about parameters GenerateConditions False whether to generate conditions on parameters Method Automatic method to use PrincipalValue False whether to use principal value integrals
Examples
open all close allBasic Examples (3)
Unilateral convolution of a function with DiracDelta:
Scope (5)
Univariate Convolution (3)
Options (2)
Applications (3)
Obtain a particular solution for a linear ordinary differential equation using convolution:
Obtain the step response of a linear, time-invariant system given its impulse response h:
The step response of the system:
Evaluate the inverse Laplace transform for the following example, using the convolution theorem:
Multiplication in the ![]() domain corresponds to a convolution operation in the
domain corresponds to a convolution operation in the ![]() domain. Begin by computing the inverse transforms for each individual term of the product:
domain. Begin by computing the inverse transforms for each individual term of the product:
Properties & Relations (7)
UnilateralConvolve computes an integral over a finite interval:
Convolution with DiracDelta gives the function itself:
Convolve coincides with UnilateralConvolve, when the input functions are causal:
The Laplace transform of a causal convolution is a product of the individual transforms:
Verify the convolution theorem for Laplace transforms on the following example:
Related Guides
History
Text
Wolfram Research (2024), UnilateralConvolve, Wolfram Language function, https://reference.wolfram.com/language/ref/UnilateralConvolve.html.
CMS
Wolfram Language. 2024. "UnilateralConvolve." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/UnilateralConvolve.html.
APA
Wolfram Language. (2024). UnilateralConvolve. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/UnilateralConvolve.html
BibTeX
@misc{reference.wolfram_2025_unilateralconvolve, author="Wolfram Research", title="{UnilateralConvolve}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/UnilateralConvolve.html}", note=[Accessed: 04-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_unilateralconvolve, organization={Wolfram Research}, title={UnilateralConvolve}, year={2024}, url={https://reference.wolfram.com/language/ref/UnilateralConvolve.html}, note=[Accessed: 04-March-2026]}