UnilateralConvolve[f,g,u,t]
给出表达式 f 和 g 关于 u 的单边卷积.
UnilateralConvolve[f,g,{u1,…,un},{t1,…,tn}]
给出多维单边卷积.


UnilateralConvolve
UnilateralConvolve[f,g,u,t]
给出表达式 f 和 g 关于 u 的单边卷积.
UnilateralConvolve[f,g,{u1,…,un},{t1,…,tn}]
给出多维单边卷积.
更多信息和选项

- UnilateralConvolve 亦称为因果卷积.
- 在查看因果系统时,自然会出现单边卷积的概念. 此类系统在任何时刻的输出仅取决于当前和过去输入的值.
- 两个函数
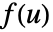 和
和 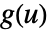 的单边卷积
的单边卷积 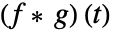 由
由 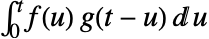 给出.
给出. - 积分的下限实际上取
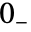 ,因此
,因此 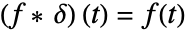 ,其中
,其中 ![TemplateBox[{{t}}, DiracDeltaSeq] TemplateBox[{{t}}, DiracDeltaSeq]](Files/UnilateralConvolve.zh/7.png) 是 DiracDelta 函数.
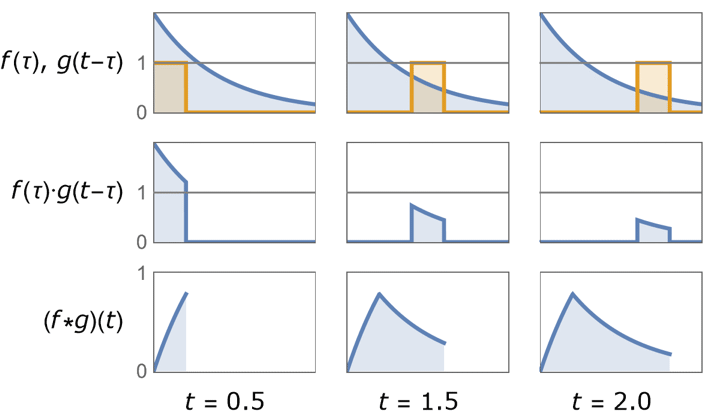
是 DiracDelta 函数. - 下面说明了指数和单位方框函数的单边卷积.
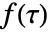 表示指数函数,
表示指数函数,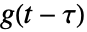 表示反射和移位单位方框函数. 卷积
表示反射和移位单位方框函数. 卷积 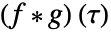 是乘积
是乘积 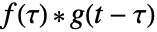 的曲线(从
的曲线(从 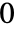 到
到 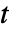 )下的面积.
)下的面积. - 多维卷积由
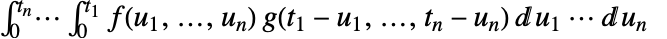 给出.
给出. - 可给出以下选项:
-
Assumptions $Assumptions 关于参数的假设 GenerateConditions False 是否生成参数的条件 Method Automatic 使用的方法 PrincipalValue False 是否使用主值积分
范例
打开所有单元 关闭所有单元基本范例 (3)
范围 (5)
应用 (3)
属性和关系 (7)
UnilateralConvolve 计算的是有限区间内的积分:
与 DiracDelta 的卷积给出函数本身:
当输入函数具有因果性时,Convolve 与 UnilateralConvolve 的结果一致:
相关指南
-
▪
- 积分变换
文本
Wolfram Research (2024),UnilateralConvolve,Wolfram 语言函数,https://reference.wolfram.com/language/ref/UnilateralConvolve.html.
CMS
Wolfram 语言. 2024. "UnilateralConvolve." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/UnilateralConvolve.html.
APA
Wolfram 语言. (2024). UnilateralConvolve. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/UnilateralConvolve.html 年
BibTeX
@misc{reference.wolfram_2025_unilateralconvolve, author="Wolfram Research", title="{UnilateralConvolve}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/UnilateralConvolve.html}", note=[Accessed: 05-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_unilateralconvolve, organization={Wolfram Research}, title={UnilateralConvolve}, year={2024}, url={https://reference.wolfram.com/language/ref/UnilateralConvolve.html}, note=[Accessed: 05-March-2026]}