WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

VarianceTest[data]

data の分散が1つであるかどうかの検定を行う．

VarianceTest[{data1,data2}]

data1と data2の分散が等しいかどうかの検定を行う．

VarianceTest[dspec,σ02]

σ02に対する分散量度の検定を行う．

VarianceTest[dspec,σ02,"property"]

"property"の値を返す．

詳細とオプション
Details and Options Details and Options
例題  
例  
スコープ  
検定  
レポート  
オプション  
AlternativeHypothesis  
SignificanceLevel  
VerifyTestAssumptions  
アプリケーション  
特性と関係  
考えられる問題  
おもしろい例題  
関連項目
関連するガイド
履歴
引用書式

VarianceTest

VarianceTest[data]

data の分散が1つであるかどうかの検定を行う．

VarianceTest[{data1,data2}]

data1と data2の分散が等しいかどうかの検定を行う．

VarianceTest[dspec,σ02]

σ02に対する分散量度の検定を行う．

VarianceTest[dspec,σ02,"property"]

"property"の値を返す．

詳細とオプション

  • VarianceTestは，帰無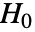仮説 と対立仮説 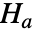で検定を行う．
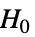
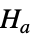
  • data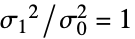
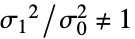
    {data1,data2}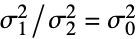
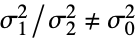
  • ただし，σi2は dataiの母分散である．
  • デフォルトで，確率値すなわち 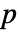値が返される．
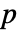  • 値が小さければ 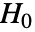が真である可能性は低い．
  • dspec 中の data は一変量{x1,x2,…}でなければならない．
  • 引数 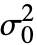は任意の正の実数でよい．
  • VarianceTest[dspec,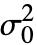]は dspec に適用可能な中で最も強力な検定を選ぶ．
  • VarianceTest[dspec,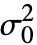,All]は dspec に適用可能なすべての検定を選ぶ．
  • VarianceTest[dspec,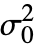,"test"]は"test"に従って 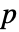値をレポートする．
  • ほとんどの検定には正規分布に従うデータが必要である．ある検定が正規性の仮説についてそれほど敏感ではない場合，その検定は強力であると呼ばれる．データが中央値について対称であると仮定する検定もある．
  • 使用可能な検定
  • "BrownForsythe"ロバスト強力なLevene検定
    "Conover"対称性data の順位の平方に基づく
    "FisherRatio"正規性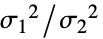に基づく
    "Levene"ロバスト,対称性個々の分散と集合の分散を比較する
    "SiegelTukey"対称性集められた data の順位に基づく
  • VarianceTest[data,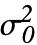,"HypothesisTestData"]はHypothesisTestDataオブジェクト htd を返す．htd["property"]を使うと追加的な検定結果と特性が抽出できる．
  • VarianceTest[data,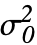,"property"]は"property"の値を直接与えるために使うことができる．
  • 検定結果のレポートに関連する特性
  • "AllTests"適用可能な検定すべてのリスト
    "AutomaticTest"Automaticが使われた場合に選ばれる検定
    "DegreesOfFreedom"検定で使われる自由度
    "PValue" 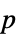値のリスト
    "PValueTable" 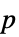値のフォーマットされた表
    "ShortTestConclusion"検定結果の短い説明
    "TestConclusion"検定結果の説明
    "TestData"検定統計と 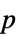値のペアのリスト
    "TestDataTable"検定統計と 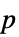値のフォーマットされた表
    "TestStatistic"検定統計のリスト
    "TestStatisticTable"検定統計のフォーマットされた表
  • 使用可能なオプション
  • AlternativeHypothesis "Unequal"対立仮説のための不等式
    SignificanceLevel 0.05診断とレポートのための切捨て
    VerifyTestAssumptions Automatic実行する診断検定を設定する
  • 分散の検定では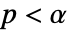， の場合にのみ 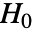が棄却されるように切捨て 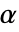が選ばれる．"TestConclusion"特性と"ShortTestConclusion"特性に使われる 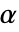の値はSignificanceLevelオプションで制御される．この値 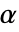は正規性診断や対称性診断を含む仮定の診断検定にも用いられる．デフォルトで 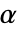は0.05に設定されている．
  • VarianceTestにおけるVerifyTestAssumptionsの名前付き設定
  • "Normality"すべてのデータが正規分布に従うことを証明する
    "Symmetry"共通の中央値について対称性を証明する

例題

すべて開く すべて閉じる

例  (3)

2つの母集団からの分散の等価性についての検定を行う：

Wolfram Language code: SeedRandom[1];data = RandomVariate[NormalDistribution[], {2, 100}];
Wolfram Language code: VarianceTest[data]

さらに特性を抽出するためにHypothesisTestDataオブジェクトを作成する：

Wolfram Language code: ℋ = VarianceTest[data, Automatic, "HypothesisTestData"]

完全な検定の表：

Wolfram Language code: ℋ["TestDataTable", All]

母分散を特定の値と比較する：

Wolfram Language code: SeedRandom[1];data = RandomVariate[NormalDistribution[1, 2], 10^3];
Wolfram Language code: VarianceTest[data, 4, "TestDataTable"]
Wolfram Language code: Variance[data]

2つの母分散比を特定の値に対して検証する：

Wolfram Language code: SeedRandom[1];data1 = RandomVariate[NormalDistribution[0, 1], 100]; data2 = RandomVariate[NormalDistribution[0, 2.5], 250];
Wolfram Language code: VarianceTest[{data1, data2}, 1 / 4, "TestDataTable"]
Wolfram Language code: Variance[data1] / Variance[data2]

対立仮説 で検定を実行する：

Wolfram Language code: VarianceTest[{data1, data2}, 1 / 4, AlternativeHypothesis -> "Less"]

スコープ  (15)

検定  (11)

母分散が1であるかどうかを検定する：

Wolfram Language code: SeedRandom[1];data1 = RandomVariate[NormalDistribution[], 500]; data2 = RandomVariate[NormalDistribution[1, 1 / 3], 500];

においては， 値は通常大きい：

Wolfram Language code: VarianceTest[data1]

が偽である場合は， 値は通常小さい：

Wolfram Language code: VarianceTest[data2]

母分散と特定の値を比べる：

Wolfram Language code: SeedRandom[2];data1 = RandomVariate[NormalDistribution[0, 2], 10^4]; data2 = RandomVariate[NormalDistribution[0, 2.1], 10^4];
Wolfram Language code: VarianceTest[data1, 2^2]
Wolfram Language code: VarianceTest[data2, 2^2]

数量データと特定の値の分散を比較する：

Wolfram Language code: SeedRandom["K"]; tempData = RandomVariate[NormalDistribution[Quantity[273, "Kelvins"], Quantity[5, "Kelvins"]], 26]
Wolfram Language code: VarianceTest[tempData, (Quantity[4.8, "Kelvins"])^2]

2つの母分散を比べる：

Wolfram Language code: SeedRandom[1];data1 = RandomVariate[NormalDistribution[], 500]; data2 = RandomVariate[StudentTDistribution[5], 500]; data3 = RandomVariate[NormalDistribution[], 350];

分散が等しい場合， 値は通常大きい：

Wolfram Language code: VarianceTest[{data1, data3}]

分散が等しくない場合， 値は通常小さい：

Wolfram Language code: VarianceTest[{data1, data2}]

2つの母分散比が特定の値であるかどうかの検定を行う：

Wolfram Language code: SeedRandom[1];data1 = RandomVariate[NormalDistribution[0, 2], 500]; data2 = RandomVariate[NormalDistribution[0, 1], 500];
Wolfram Language code: Subscript[σ, 0] = 4;

以下の形式は等しい：

Wolfram Language code: VarianceTest[{data2, data1}, 1 / Subscript[σ, 0]]
Wolfram Language code: VarianceTest[{data1, data2}, Subscript[σ, 0]]

を決定する場合には，データ集合の順序を考慮すべきである：

Wolfram Language code: VarianceTest[{data2, data1}, Subscript[σ, 0]]

Automaticを使うと，一般に最も強力で適切な検定が適用される：

Wolfram Language code: SeedRandom[1];data = RandomVariate[NormalDistribution[], {2, 10^4}];
Wolfram Language code: VarianceTest[data, 1, Automatic]

特性"AutomaticTest"は，どの検定が選ばれたのかを調べるのに使える：

Wolfram Language code: VarianceTest[data, 1, "AutomaticTest"]

等分散について特定の検定を行う：

Wolfram Language code: SeedRandom[1];data = RandomVariate[NormalDistribution[], {2, 10^3}];
Wolfram Language code: VarianceTest[data, 1, "BrownForsythe"]

任意数の検定を同時に行うことができる：

Wolfram Language code: VarianceTest[data, 1, {"PValue", {"Levene", "BrownForsythe"}}]

データに適切な検定をすべて同時に行う：

Wolfram Language code: SeedRandom[1];data = RandomVariate[NormalDistribution[], {2, 250}];
Wolfram Language code: VarianceTest[data, 1, All]

特性"AllTests"を使ってどの検定が使われたのかを調べる：

Wolfram Language code: VarianceTest[data, 1, "AllTests"]

繰り返し特性を抽出するためにHypothesisTestDataオブジェクトを作成する：

Wolfram Language code: SeedRandom[1];data = RandomVariate[NormalDistribution[], {2, 10^4}];
Wolfram Language code: ℋ = VarianceTest[data, 1, "HypothesisTestData"];

抽出に使用できる特性：

Wolfram Language code: ℋ["Properties"]

HypothesisTestDataオブジェクトから特性をいくつか抽出する：

Wolfram Language code: SeedRandom[2];data = RandomVariate[NormalDistribution[], {2, 10^4}];
Wolfram Language code: ℋ = VarianceTest[data, 1, "HypothesisTestData"];

ルベーン(Levene)検定からの 値と検定統計：

Wolfram Language code: ℋ["PValue", "Levene"]
Wolfram Language code: ℋ["TestStatistic", "Levene"]

任意数の特性を同時に抽出する：

Wolfram Language code: SeedRandom[1];data = RandomVariate[NormalDistribution[], {2, 100}];
Wolfram Language code: ℋ = VarianceTest[data, 1, "HypothesisTestData"];

Brown–Forsythe検定からの 値と検定統計：

Wolfram Language code: ℋ[{{"PValue", "BrownForsythe"}, {"TestStatistic", "BrownForsythe"}}]

レポート  (4)

いくつかの検定からの結果を表にする：

Wolfram Language code: SeedRandom[1];data = RandomVariate[NormalDistribution[], {2, 10^3}];
Wolfram Language code: ℋ = VarianceTest[data, 1, "HypothesisTestData"];
Wolfram Language code: ℋ["TestDataTable"]

適切な検定結果すべての完全な表：

Wolfram Language code: ℋ["TestDataTable", All]

選択された検定結果の表：

Wolfram Language code: ℋ["TestDataTable", {"Conover", "BrownForsythe"}]

カスタマイズしたレポート用に検定表から項目を取り出す：

Wolfram Language code: data = BlockRandom[SeedRandom[1];RandomVariate[NormalDistribution[], {2, 10^3}]];
Wolfram Language code: ℋ = VarianceTest[data, 1, "HypothesisTestData"];
Wolfram Language code: res = ℋ["TestData", All];
Wolfram Language code: ℋ["AllTests"]

値が0.05より大きいので，このレベルでは正規性を退けるのに十分な証拠はない：

Wolfram Language code: Show[BarChart[res[[All, 2]], ChartLabels -> Placed[ℋ["AllTests"], Center], BarOrigin -> Left], Graphics[{Dashed, InfiniteLine[{{.05, 0}, {.05, 1}}]}]]

検定あるいは検定グループの 値を表にする：

Wolfram Language code: SeedRandom[2];data = RandomVariate[NormalDistribution[], {2, 10^4}];
Wolfram Language code: ℋ = VarianceTest[data, 1, "HypothesisTestData"];
Wolfram Language code: ℋ["PValueTable", "Levene"]

表の 値：

Wolfram Language code: ℋ["PValue", "Levene"]

すべての適切な検定の 値の表：

Wolfram Language code: ℋ["PValueTable", All]

検定の一部からの 値の表：

Wolfram Language code: ℋ["PValueTable", {"Levene", "Conover", "BrownForsythe"}]

検定あるいは検定グループからの検定統計をレポートする：

Wolfram Language code: SeedRandom[1];data = RandomVariate[CauchyDistribution[1, 2], {2, 10^3}];
Wolfram Language code: ℋ = VarianceTest[data, 1, "HypothesisTestData"];
Wolfram Language code: ℋ["TestStatisticTable"]

表からの検定統計：

Wolfram Language code: ℋ["TestStatistic"]

すべての適切な検定からの検定統計の表：

Wolfram Language code: ℋ["TestStatisticTable", All]

オプション  (10)

AlternativeHypothesis  (3)

デフォルトで両側検定が行われる：

Wolfram Language code: SeedRandom[1]; data = RandomVariate[NormalDistribution[], 100];

対 を検定する：

Wolfram Language code: VarianceTest[data, 1, AlternativeHypothesis -> "Unequal"]
Wolfram Language code: VarianceTest[data, 1, AlternativeHypothesis -> Automatic]

両側検定を行う．あるいは片側検定を代りに行う：

Wolfram Language code: SeedRandom[1];data = RandomVariate[NormalDistribution[0, 1.25], 100];

対 を検定する：

Wolfram Language code: VarianceTest[data, Automatic, AlternativeHypothesis -> "Unequal"]

対 を検定する：

Wolfram Language code: VarianceTest[data, Automatic, AlternativeHypothesis -> "Less"]

対 を検定する：

Wolfram Language code: VarianceTest[data, Automatic, AlternativeHypothesis -> "Greater"]

ヌル値が与えられている場合に，片側検定を代りに行う：

Wolfram Language code: SeedRandom[1];data1 = RandomVariate[NormalDistribution[0, .9], 100]; data2 = RandomVariate[NormalDistribution[0, 1], 100];
Wolfram Language code: Variance[data1] / Variance[data2]

対 を検定する：

Wolfram Language code: VarianceTest[{data1, data2}, 1, AlternativeHypothesis -> "Less"]

対 を検定する：

Wolfram Language code: VarianceTest[{data1, data2}, 1.5, AlternativeHypothesis -> "Less"]

SignificanceLevel  (3)

診断検定の有意水準を設定する：

Wolfram Language code: SeedRandom[1];data = BlockRandom[SeedRandom[5];RandomVariate[StudentTDistribution[3], 50]];
Wolfram Language code: VarianceTest[data, 1, "FisherRatio", SignificanceLevel -> .005]

デフォルトで0.05が使われる：

Wolfram Language code: VarianceTest[data, 1, "FisherRatio", SignificanceLevel -> Automatic]

有意水準を設定することによって自動的にどの検定が選ばれるかが変わることがある：

Wolfram Language code: data = BlockRandom[SeedRandom[1];RandomVariate[StudentTDistribution[3], {2, 50}]];
Wolfram Language code: VarianceTest[data, 1, "AutomaticTest", SignificanceLevel -> .0001]

順位に基づく検定がデフォルトでは選ばれたはずである：

Wolfram Language code: VarianceTest[data, 1, "AutomaticTest", SignificanceLevel -> Automatic]

有意水準は"TestConclusion"と"ShortTestConclusion"にも使われる：

Wolfram Language code: data = BlockRandom[SeedRandom[1];RandomVariate[NormalDistribution[0, 1], 100]];
Wolfram Language code: ℋ1 = VarianceTest[data, 1.5, "HypothesisTestData", SignificanceLevel -> .05];
Wolfram Language code: ℋ2 = VarianceTest[data, 1.5, "HypothesisTestData", SignificanceLevel -> .01];
Wolfram Language code: ℋ1["TestConclusion"]//TraditionalForm
Wolfram Language code: ℋ2["TestConclusion"]//TraditionalForm
Wolfram Language code: ℋ1["ShortTestConclusion"]
Wolfram Language code: ℋ2["ShortTestConclusion"]

VerifyTestAssumptions  (4)

診断は，AllかNoneを使ってまとめて制御することができる：

Wolfram Language code: SeedRandom[1];data1 = RandomVariate[StudentTDistribution[3], 1000]; data2 = RandomVariate[NormalDistribution[0, Sqrt[3]], 1000];

すべての仮定を検証する：

Wolfram Language code: VarianceTest[{data1, data2}, 1 / 4, "Levene", VerifyTestAssumptions -> All]

どの仮定もチェックしない：

Wolfram Language code: VarianceTest[{data1, data2}, 1 / 4, "Levene", VerifyTestAssumptions -> None]

診断は個々に制御することができる：

Wolfram Language code: SeedRandom[2];data1 = RandomVariate[StudentTDistribution[3], 1000]; data2 = RandomVariate[NormalDistribution[0, Sqrt[3]], 1000];

正規性を仮定するが，対称性についてチェックする：

Wolfram Language code: VarianceTest[{data1, data2}, 1 / 4, "Levene", VerifyTestAssumptions -> "Symmetry"]

正規性についてのみチェックする：

Wolfram Language code: VarianceTest[{data1, data2}, 1 / 4, "Levene", VerifyTestAssumptions -> "Normality"]

検定の仮定値は明示的に設定することができる：

Wolfram Language code: data = RandomVariate[CauchyDistribution[0, 1], 100];
Wolfram Language code: VarianceTest[data, 1, "TestDataTable"]
Wolfram Language code: VarianceTest[data, 1, "TestDataTable", VerifyTestAssumptions -> "Normality" -> True]

シミュレーションを行う場合は，診断検定を行わないようにすると有益であることが多い：

Wolfram Language code: data = RandomVariate[NormalDistribution[], {1000, 100}];
Wolfram Language code: AbsoluteTiming[T = Quiet@VarianceTest[#, Automatic, {"TestStatistic", "FisherRatio"}]& /@ data;]

検定の仮定は意図的に有効になっているので，時間が大幅に短縮できる：

Wolfram Language code: AbsoluteTiming[T2 = Quiet@VarianceTest[#, Automatic, {"TestStatistic", "FisherRatio"}, VerifyTestAssumptions -> None]& /@ data;]

結果は全く同じである：

Wolfram Language code: SmoothHistogram[{T, T2}]

アプリケーション  (2)

ある母分散が等しいかどうかについて検定を行う：

Wolfram Language code: SeedRandom[1];data1 = RandomVariate[NormalDistribution[0, 1], 100]; data2 = RandomVariate[NormalDistribution[0, 1], 100]; data3 = RandomVariate[NormalDistribution[0, 3], 100];
Wolfram Language code: BoxWhiskerChart[{data1, data2, data3}, "Notched", ChartStyle -> "SolarColors"]

最初の2つの母集団は似た分散を持つ：

Wolfram Language code: VarianceTest[{data1, data2}, Automatic, "TestDataTable"]

3つ目の母集団は1つ目とは異なる分散を持つ：

Wolfram Language code: VarianceTest[{data1, data3}, Automatic, "TestDataTable"]

2つの異なるクラスで25人の小学生が，長さ2.15cmのものを同じ定規を使って測った：

Wolfram Language code: group1 = {2.28, 2.13, 2.21, 2., 2.06, 2.09, 2.12, 2.27, 2.17, 2.09, 2.02, 2.28, 2.28, 2.03, 2.11, 2.05, 2.06, 2.28, 2.1, 2.35, 2.07, 2.22, 2.19, 2.33, 2.02};
Wolfram Language code: group2 = {2.03, 2.12, 1.92, 1.96, 2.05, 2.05, 2.02, 2.12, 2.02, 1.95, 2., 2.03, 1.93, 1.96, 2.08, 1.92, 2.12, 2.01, 1.84, 2.06, 2., 1.95, 1.90, 2., 1.94};
Wolfram Language code: {Variance[group1], Variance[group2]}

2つ目の群は精度の面で優れている：

Wolfram Language code: VarianceTest[{group1, group2}, 1, "TestDataTable"]

二乗誤差を使って群の確度を比較する：

Wolfram Language code: SqrErr1 = (group1 - 2.15)^2;SqrErr2 = (group2 - 2.15)^2;
Wolfram Language code: {Mean[SqrErr1], Mean[SqrErr2]}

1つ目の群の方がずっと確度が高い：

Wolfram Language code: LocationTest[{SqrErr1, SqrErr2}, 0, "TestDataTable"]

特性と関係  (7)

値は，誤陽性（タイプIエラー）の予想される割合を示唆する：

Wolfram Language code: data = RandomVariate[NormalDistribution[], {1000, 10}];
Wolfram Language code: pvals = Table[VarianceTest[i, 1, "FisherRatio", VerifyTestAssumptions -> None], {i, data}];

検定のサイズを0.05に設定すると，5%の割合で が誤って退けられる結果になる：

Wolfram Language code: Probability[x ≤ 0.05, xpvals]//N

各検定の力は，が偽である場合にそれを退ける確率である：

Wolfram Language code: n = 100;
Wolfram Language code: data1 = RandomVariate[NormalDistribution[0, .75], {1000, n}]; data2 = RandomVariate[NormalDistribution[0, 1], {1000, n}];
Wolfram Language code: tests = VarianceTest[{data1[[1]], data2[[1]]}, 1, "AllTests"]
Wolfram Language code: pvs = MapThread[VarianceTest[{#1, #2}, 1, tests, VerifyTestAssumptions -> None]&, {data1, data2}];
Wolfram Language code: α = {.001, .005, .01, .025, .05, .1};

6つの異なるレベルにおける検定の力．Siegel–Tukey検定が最も低い力を持つ：

Wolfram Language code: Grid[Join[{Join[{""}, α]}, Table[Join[{tests[[i]]}, (Probability[x ≤ #1, xpvs[[All, i]]]&) /@ α], {i, Length[tests]}]], Alignment -> Left, Background -> {None, {StandardGray, {StandardBlue, StandardPink}}}, Dividers -> {{False, True}, {False, True}}]//N

検定の力はサンプルサイズに比例する：

Wolfram Language code: n = 10;
Wolfram Language code: data1 = RandomVariate[NormalDistribution[0, .75], {1000, n}]; data2 = RandomVariate[NormalDistribution[0, 1], {1000, n}];
Wolfram Language code: tests = VarianceTest[{data1[[1]], data2[[1]]}, 1, "AllTests"]
Wolfram Language code: pvs = MapThread[VarianceTest[{#1, #2}, 1, tests, VerifyTestAssumptions -> None]&, {data1, data2}];
Wolfram Language code: α = {.001, .005, .01, .025, .05, .1};

検定の力は上の例におけるものよりも低い：

Wolfram Language code: Grid[Join[{Join[{""}, α]}, Table[Join[{tests[[i]]}, (Probability[x ≤ #1, xpvs[[All, i]]]&) /@ α], {i, Length[tests]}]], Alignment -> Left, Background -> {None, {StandardGray, {StandardPurple, StandardBlue}}}, Dividers -> {{False, True}, {False, True}}]//N

両側の 値は，片側の 値の半分である：

Wolfram Language code: data1 = RandomVariate[NormalDistribution[0, 1], 100]; data2 = RandomVariate[NormalDistribution[0, .5], 100];
Wolfram Language code: twoSided = VarianceTest[{data1, data2}, 1, All, AlternativeHypothesis -> "Unequal"];
Wolfram Language code: minOneSided = Min /@ Transpose[{VarianceTest[{data1, data2}, 1, All, AlternativeHypothesis -> "Less"], VarianceTest[{data1, data2}, 1, All, AlternativeHypothesis -> "Greater"]}];
Wolfram Language code: twoSided - 2 minOneSided

Brown–Forsythe検定とルベーン(Levene)検定は1つのサンプルについてフィッシャー(Fisher)の比率検定に等しい：

Wolfram Language code: data = RandomVariate[NormalDistribution[], 100];
Wolfram Language code: VarianceTest[data, Automatic, {"TestDataTable", {"FisherRatio", "BrownForsythe", "Levene"}}]

分散検定は，入力がTimeSeriesのときにのみ値に使うことができる：

Wolfram Language code: ts = TemporalData[TimeSeries, {{{1.224578634529677, 0.47929635789978015, 0.6572781300178168, 0.21496048742669355, 0.7299608014554928, -0.2495111111278263, -1.3286551762002712, 0.552725018274874, 0.19272112205837066, 1.1809144012420882, -1.1671 ... 40938613662046, 1.052394590214582, 0.9345044123980388, 0.38537803109557855, -0.48660931166089394, -0.71203560340161}}, {{0, 100, 1}}, 1, {"Continuous", 1}, {"Discrete", 1}, 1, {ValueDimensions -> 1, ResamplingMethod -> None}}, False, 10.1];
Wolfram Language code: VarianceTest[ts, Automatic, {"TestDataTable", All}]
Wolfram Language code: VarianceTest[ts["Values"], Automatic, {"TestDataTable", All}]
Wolfram Language code: %% == %

分散検定は，入力がTemporalDataのときはすべての値に同時に使うことができる：

Wolfram Language code: td = TemporalData[Automatic, {{{-0.25275046867718637, -0.7175779198306353, -1.9370139837317764, 0.006665621735740701, -0.3730807122324292, 0.6740106823161018, 0.8562214990564344, 0.955785083955732, 1.7020898014886303, 1.8523009430646802, 0.244 ... 3951759101545, -1.1611722313627828, 1.1602446901533021, 1.1052173095128992, 1.1089143920161917, -0.13837156328402}}, {{0, 100, 1}}, 2, {"Continuous", 2}, {"Discrete", 1}, 1, {ValueDimensions -> 1, ResamplingMethod -> None}}, False, 10.1];
Wolfram Language code: VarianceTest[td]

すべての値のみについての検定を行う：

Wolfram Language code: data = td["ValueList"]//Flatten; VarianceTest[data]

2つの経路の分散が等しいかどうかの検定を行う：

Wolfram Language code: {data1, data2} = td["ValueList"];
Wolfram Language code: VarianceTest[{data1, data2}]

考えられる問題  (2)

Conover検定とSiegel–Tukey検定は1つのサンプルについては定義されない：

Wolfram Language code: data = RandomVariate[NormalDistribution[], 100];
Wolfram Language code: VarianceTest[data, Automatic, {"TestDataTable", {"Conover", "SiegelTukey"}}]

検定の中には正規分布に従うことを仮定するものもある：

Wolfram Language code: data = RandomVariate[LaplaceDistribution[1, 2], {2, 100}];
Wolfram Language code: VarianceTest[data, Automatic, {"TestDataTable", {"BrownForsythe", "FisherRatio", "Levene"}}]

Conover検定とSiegel–Tukey検定は正規性を仮定しない：

Wolfram Language code: VarianceTest[data, Automatic, {"TestDataTable", {"Conover", "SiegelTukey"}}]

おもしろい例題  (1)

帰無仮説 が真であるときの統計量を計算する：

Wolfram Language code: data = RandomVariate[NormalDistribution[], {250, 100}];
Wolfram Language code: T1 = VarianceTest[#, 1, "TestStatistic", VerifyTestAssumptions -> None]& /@ data;

特定の対立仮説による検定統計：

Wolfram Language code: T2 = VarianceTest[#, 2, "TestStatistic", VerifyTestAssumptions -> None]& /@ data;

検定統計の分布を比較する：

Wolfram Language code: SmoothHistogram[{T1, T2}, Filling -> Axis, PlotLegends -> {"SubscriptBox[H, 0] is True", "SubscriptBox[H, 0] is False"}]
Wolfram Research (2010), VarianceTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/VarianceTest.html.

テキスト

Wolfram Research (2010), VarianceTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/VarianceTest.html.

CMS

Wolfram Language. 2010. "VarianceTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/VarianceTest.html.

APA

Wolfram Language. (2010). VarianceTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/VarianceTest.html

BibTeX

@misc{reference.wolfram_2026_variancetest, author="Wolfram Research", title="{VarianceTest}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/VarianceTest.html}", note=[Accessed: 10-October-2026]}

BibLaTeX

@online{reference.wolfram_2026_variancetest, organization={Wolfram Research}, title={VarianceTest}, year={2010}, url={https://reference.wolfram.com/language/ref/VarianceTest.html}, note=[Accessed: 10-October-2026]}