VonMisesStress

VonMisesStress[vars,pars,stress]

stress から vonMises応力を与える．

詳細

  • vonMises応力測度は，延性材料が応力下で降伏するかどうかを予測するために使用される．
  • vonMises応力は，最大歪みエネルギーとしても知られている．
  • vonMises応力は，断面積 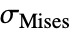（単位： [TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 2}}, newtons per meter squared, {{(, "Newtons", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]]）あたりの圧力である．
  • VonMisesStressは，SolidMechanicsPDEComponentにおけるのと同じ変数 vars 指定を使う．
  • VonMisesStressは，SolidMechanicsPDEComponentにおけるのと同じパラメータ pars 指定を使う．
  • stress はSymmetrizedArrayを介して指定される．
  • 通常，stress SymmetrizedArrayは3 x 3次元で対称でなければならない．
  • 通常，stress はSolidMechanicsStressの結果である．
  • VonMisesStressは以下を計算する：
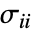  • は法線応力を表し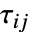，はせん断応力を表す．

例題

すべて開くすべて閉じる

例  (2)

応力テンソルのvonMises応力を計算する：

梁上の負荷が材料の降伏限界を超えていないかどうかを計算する．梁を作成する：

変数と材料パラメータを設定する：

梁は左端が固定されており，右端には下方向に100ニュートンの負荷がかけられている．この負荷による梁の変位を計算する：

この変位による歪みと応力を計算する：

vonMises応力を計算する：

vonMises応力を可視化する：

vonMises応力の最大値を求める：

vonMises応力の最大値が材料の降伏力より小さいかどうかチェックする：

スコープ  (3)

歪みを通してvonMises応力を表現する．歪みから応力を計算する：

vonMises応力を計算する：

vonMises応力を変位を通して表現する．変位から歪みを計算する：

歪みからの応力を計算する：

vonMises応力を計算する：

チタン梁のような構造のvonMises応力に基づく破壊基準を調べる．

梁の幾何形状を設定する：

変数と材料パラメータを設定する：

偏微分方程式を設定して解く：

変位による歪みを計算する：

歪みからの応力を計算する：

応力テンソルからのvonMises応力を計算する：

変形した物体上のvonMises応力の強度を可視化する：

梁の破損しやすい部分を見付けるために，材料の降伏限界に対するvonMises応力の値に基準を適用する．材料の引張降伏強度を求める：

破損する可能性があるのは，極限値より上の応力がある領域だけである：

破損する可能性がある領域を可視化する：

アプリケーション  (5)

定常解析  (1)

スプーンの端を固定して上部に力を加えたときのたわみを計算する．変数とパラメータを設定する：

偏微分方程式と幾何形状を設定する：

変位による歪みを計算する：

歪みからの応力を計算する：

歪みテンソルからvonMises応力を計算する：

vonMises応力を可視化する：

超弾性定常解析  (3)

超弾性材料のオブジェクト内のvonMises応力を計算する．変数と材料の特性を設定する：

形状を指定する：

形状は左の辺に固定され，右の辺上で右に引っ張られる．この変位についての偏微分方程式を解く：

変位による歪みを計算する：

歪みと変異による応力を計算する：

応力テンソルからvonMise応力を計算する：

スケールされ変形されたオブジェクト内のvonMises応力を可視化する：

超弾性材料でできた3Dオブジェクト内のvonMises応力を計算する．変数と材料特性を設定する：

形状を指定する：

形状は左辺に固定され，右辺で右に引っ張られる．疎なメッシュによる変位についての偏微分方程式を解く：

変位による歪みを計算する：

歪みと変位による応力とそれにかかる時間を計算する：

応力テンソルからvonMises応力を計算する：

スケールされ変形されたオブジェクト内のvonMises応力を可視化する：

トルクを受ける整形外科手術に使用されるチタン固定プレートのvonMises応力に基づく破損基準を調べる．

典型的な前腕固定プレートの形状を設定する：

変数と材料パラメータを設定する：

プレートは16×1×0.3TemplateBox[{InterpretationBox[, 1], "cm", centimeters, "Centimeters"}, QuantityTF]で，穴がいくつか開いている．最初の4分の1が固定され，最後の4分の1がトルクを受ける設定を考えてみる：

偏微分方程式を設定して解く：

変位による歪みを計算する：

歪みによる応力を計算する：

応力テンソルによるvonMises応力を計算する：

変形した物体上のvonMisesの応力強度を可視化する：

固定プレートの破損しやすい領域を見付けるために，材料の降伏限界に対するvonMises応力の値に基準を適用する．材料の引張降伏強度を調べる：

限界値を超える応力がかかった領域のみが破損する可能性がある：

破損する可能性がある領域を可視化する：

繊維強化超弾性定常解析  (1)

左側が固定されて右側に圧力が加えられた繊維強化ゴム片の変数とモデルパラメータを設定する．ネオフック超弾性材料モデルが使用される：

形状を設定する：

形状内の繊維強化を可視化する：

方程式を設定して変位について解く：

変形された物体ともとの物体の形状を可視化する：

歪みを計算する：

応力を計算する：

vonMises応力を計算する：

vonMises応力を可視化する：

考えられる問題  (1)

2 x 2 応力テンソルを使うことができる：

例えば平面歪みの場合，3番目の方向に依然としてゼロ以外の応力が存在する可能性があるため，ここでは注意が必要である．これについては，固体力学モノグラフの「平面歪み，平面応力，軸対称モデル」のセクションで説明されている．ただし，3 x 3 の応力テンソルを使用した2次元変数設定を使用することは可能である：

Wolfram Research (2024), VonMisesStress, Wolfram言語関数， https://reference.wolfram.com/language/ref/VonMisesStress.html.

テキスト

Wolfram Research (2024), VonMisesStress, Wolfram言語関数， https://reference.wolfram.com/language/ref/VonMisesStress.html.

CMS

Wolfram Language. 2024. "VonMisesStress." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/VonMisesStress.html.

APA

Wolfram Language. (2024). VonMisesStress. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/VonMisesStress.html

BibTeX

@misc{reference.wolfram_2024_vonmisesstress, author="Wolfram Research", title="{VonMisesStress}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/VonMisesStress.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_vonmisesstress, organization={Wolfram Research}, title={VonMisesStress}, year={2024}, url={https://reference.wolfram.com/language/ref/VonMisesStress.html}, note=[Accessed: 21-November-2024 ]}