VonMisesStress
VonMisesStress[vars,pars,stress]
生成 stress 的冯·米赛斯应力.
更多信息

- 冯·米赛斯应力准则被广泛用于预测延性材料在应力作用下是否会发生屈服.
- 冯·米赛斯应力也称为最大畸变能.
- 冯·米赛斯应力
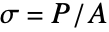 的单位为压强 [
的单位为压强 [![TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF]](Files/VonMisesStress.zh/2.png) ].
]. - VonMisesStress 使用与 SolidMechanicsPDEComponent 相同的变量 vars 规范.
- VonMisesStress 使用与 SolidMechanicsPDEComponent 相同的参数 pars 规范.
- stress 通过 SymmetrizedArray 指定.
- 通常,stress SymmetrizedArray 的维度为 3 x 3,并且必须是对称的.
- 通常,stress 是 SolidMechanicsStress 的结果.
- VonMisesStress 计算:
- 其中,
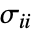 代表法向应力,
代表法向应力,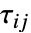 代表剪应力.
代表剪应力.
范例
打开所有单元关闭所有单元基本范例 (2)
范围 (3)
应用 (5)
稳态分析 (1)
超弹性稳态分析 (3)
可能存在的问题 (1)
在平面应变情况下,第三方向上可能仍然存在非零应力. 这在固体力学专著的“平面应变、平面应力和轴对称模型”一节中进行了解释. 然而,可以使用具有 3 x 3 应力张量的二维变量设置:
Wolfram Research (2024),VonMisesStress,Wolfram 语言函数,https://reference.wolfram.com/language/ref/VonMisesStress.html (更新于 2025 年).
文本
Wolfram Research (2024),VonMisesStress,Wolfram 语言函数,https://reference.wolfram.com/language/ref/VonMisesStress.html (更新于 2025 年).
CMS
Wolfram 语言. 2024. "VonMisesStress." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2025. https://reference.wolfram.com/language/ref/VonMisesStress.html.
APA
Wolfram 语言. (2024). VonMisesStress. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/VonMisesStress.html 年