WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

"SpanningTree" (Machine Learning Method)

Details & Suboptions

  • "SpanningTree" is a neighbor-based clustering method. "SpanningTree" works for arbitrary cluster shapes and sizes; however, it can fail when clusters have different densities or are loosely connected.
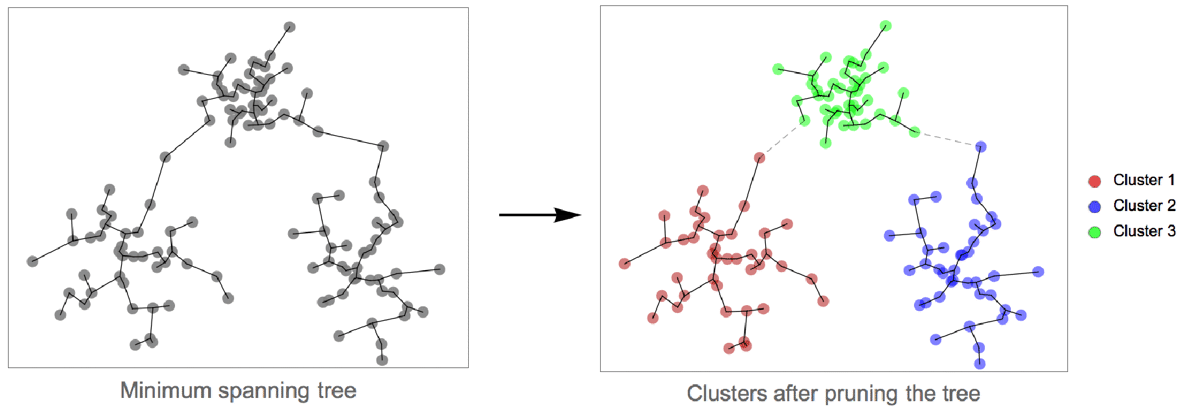
  • The following plots show the results of the "SpanningTree" method applied to toy datasets:
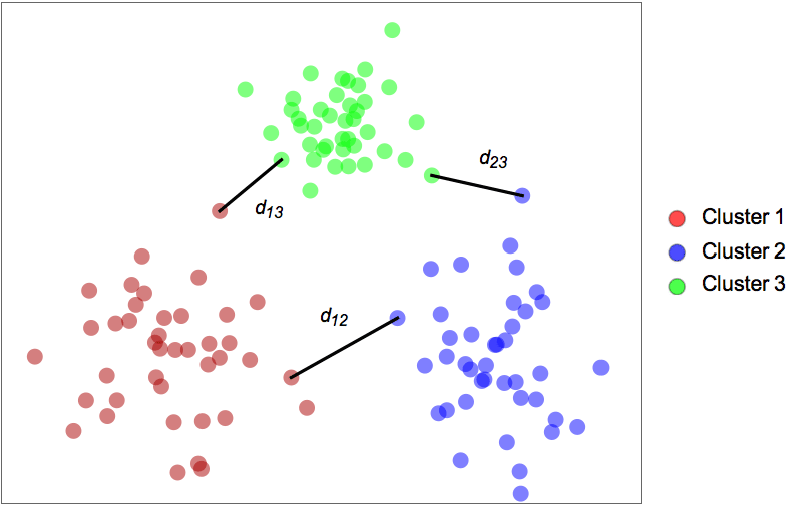
  • The algorithm finds the set of clusters for which neighboring clusters are the most distant from each other. The distance dij between two neighboring clusters i and j is defined as the distance between their closest points:
  • Formally, the "SpanningTree" method constructs the minimum spanning tree of data points (using distances as graph weights). The longest edges of the tree are then pruned. Each connected component corresponds to a cluster. The pruning stops when the specified number of clusters is reached. When the number of clusters is not specified, the pruning stops when all edges are shorter than a given threshold.
  • The option DistanceFunction can be used to define which distance to use.
  • The following suboption can be given:
  • "MaxEdgeLength" Automaticpruning length threshold

Examples

open allclose all

Basic Examples  (3)Summary of the most common use cases

Find clusters of nearby values using the "SpanningTree" method:

In[1]:=1
✖
https://wolfram.com/xid/0ffcxe9qcqdbg-wxc5bs
Out[1]=1
In[1]:=1
✖
https://wolfram.com/xid/0ffcxe9qcqdbg-3sq4zb
Out[1]=1

Train the ClassifierFunction using the "SpanningTree" method:

In[2]:=2
✖
https://wolfram.com/xid/0ffcxe9qcqdbg-0wodlh
Out[2]=2

Obtain the cluster assignment and cluster the data:

In[3]:=3
✖
https://wolfram.com/xid/0ffcxe9qcqdbg-s8b4j2
Out[3]=3
Out[3]=3

Create random 2D vectors:

In[1]:=1
✖
https://wolfram.com/xid/0ffcxe9qcqdbg-q8s2rm
Out[1]=1

Plot clusters identified by the "SpanningTree" method:

In[2]:=2
✖
https://wolfram.com/xid/0ffcxe9qcqdbg-fj7crm
Out[2]=2

Scope  (2)Survey of the scope of standard use cases

Find cluster indices using ClusteringComponents:

In[1]:=1
✖
https://wolfram.com/xid/0ffcxe9qcqdbg-ms4t02
Out[1]=1

Create and visualize noisy 2D moon-shaped training and test datasets:

In[1]:=1
✖
https://wolfram.com/xid/0ffcxe9qcqdbg-f8bvfg
Out[1]=1

Train a ClassifierFunction using "SpanningTree" and find clusters in the test set:

In[2]:=2
✖
https://wolfram.com/xid/0ffcxe9qcqdbg-xpxr9m
Out[2]=2

Visualizing two intertwined clusters found by "SpanningTree":

In[3]:=3
✖
https://wolfram.com/xid/0ffcxe9qcqdbg-ultqo9
Out[3]=3

Options  (2)Common values & functionality for each option

DistanceFunction  (1)

Cluster data using Manhattan distance:

In[1]:=1
✖
https://wolfram.com/xid/0ffcxe9qcqdbg-xbfrhk
Out[1]=1

"MaxEdgeLength"  (1)

Find clusters by specifying the "MaxEdgeLength" suboption:

In[1]:=1
✖
https://wolfram.com/xid/0ffcxe9qcqdbg-itcrji
Out[1]=1