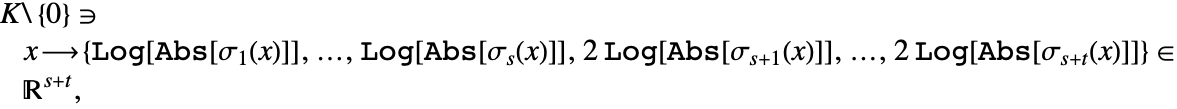代数数域

Wolfram 语言以 Root 对象的形式表示代数数（algebraic number）. 一个 Root 对象包含了代数数的最小多项式和根数（root number）. 根数是一个整数，用于表明 Root 对象所表示的是最小多项式的哪个根. 这样是为了使任意复数代数数的表示唯一. 一个缺点是用这样的表示进行代数运算要付出很大的代价. 这也是为什么 Wolfram 语言要求使用一个附加的函数，RootReduce，来简化运算表达式. 将计算限制在有理数的一个固定的有限的代数扩张（algebraic extension） 内，可以将其中的元素更加方便地表示为关于 的一个多项式.

AlgebraicNumber[θ,{c0,c1,…,cn}]表示 中的代数数

以有理数有限扩张的元素的形式表示代数数.

若 为一代数整数，具有次数为 的最小多项式，且 、…、 为有理数，则AlgebraicNumber[θ,{c0,…,cl}] 为一惰性数字对象（inert numeric object）：
N 可以用来求 AlgebraicNumber 对象的数值近似：

对于任何代数数 和有理数列表 、…、，AlgebraicNumber[θ,{c0,…,cl}] 计算给出AlgebraicNumber[ξ,{d0,…,dm}]，其中 是一个代数整数，对于 的最小多项式的首系数的某个因子 ，满足 ， 是 的最小多项式的次数，且

AlgebraicNumber 自动产生一个代数整数的生成器以及长度等于该扩张的次数的系数列表：
表示有理数的 AlgebraicNumber 对象自动约化为数：
加上或者乘以明确属于同一域（即具有相同的第一元素）的 AlgebraicNumber 对象，加上或者乘以一个有理数和一个 AlgebraicNumber 对象，或者将 AlgebraicNumber 对象提升至一个整数幂，都得到一个 AlgebraicNumber 对象：
RootReduce 将 AlgebraicNumber 对象变换为一个 Root 对象：
ToNumberField[a,θ]将代数数 a 在 θ 所生成的数域上表示
ToNumberField[{a1,a2,…},θ]将 ai 在 θ 所生成的域上表示
ToNumberField[{a1,a2,…}]将 ai 在由单一代数数生成的公共扩张域（common extension field ）上表示

以代数数域元素的形式表示任意代数数.

ToNumberField 可以用来找到含有给定代数数的有理数的公共有限扩张（common extension field ）：
这里将 用 Root[1-10 #12+#14&,4] 生成的一个域元素表示：

与在全体复数代数数域上进行运算相比，在有理数的一个固定的有限扩张上进行运算要快得多.

假设要找到有理函数 f 的值，其中 {x,y,z} 被代数数 {a,b,c} 取代：
使用 RootReduce 在 {a,b,c} 处直接计算 f 的值需要的时间很长：
一个较快的方法是在包含 {a,b,c} 的一个公共代数数域内进行计算：
在公共数域内部的运算要快得多：
将所得的 AlgebraicNumber 对象转化为一个 Root 对象也同样很快：

ToNumberField[{a1,a2,…}] 等价于 ToNumberField[{a1,a2,…},Automatic]，它不一定使用最小公共域扩张. 而 ToNumberField[{a1,a2,…},All] 始终使用最小公共域扩张.

此处第一个 AlgebraicNumber 对象等于 ，因此不生成在其上表示它的4次域 (Root[1-10 #12+#14&,4]). 然而，由 ToNumberField 得到的公共域包含全部域 (Root[1-10 #12+#14&,4])：
第二个参数 All 的设定使得 ToNumberField 寻找可能的最小域成：
MinimalPolynomial[a]给出代数数 a 在整数上的最小多项式的纯函数表示
MinimalPolynomial[a,x]以 x 的多项式的形式给出代数数 a 的最小多项式
AlgebraicIntegerQ[a]若代数数 a 为一代数整数返回 True，否则返回 False
AlgebraicNumberDenominator[a]给出最小正整数 n 使得 na 为一代数整数
AlgebraicNumberTrace[a]给出代数数 a 的迹（trace）
AlgebraicNumberNorm[a]给出代数数 a 的范数（norm）
AlgebraicUnitQ[a]若代数数 a 为一代数单位元，返回 True，否则返回 False
RootOfUnityQ[a]若代数数 a 是一个单位根，返回 True，否则返回 False

计算代数数性质的函数.

一个代数数 的最小多项式是一个带有整数系数和最小整数首系数的次数最低的多项式 ，使得 .

这里给出了以纯函数表示的 的最小多项式：
这里给出了以关于 x 的多项式表示的 Root[#15-2 #1+7&,1]2+1 的最小多项式：

当且仅当一个代数数的 MinimalPolynomial 首一（monic）时，该代数数为代数整数.

此处表明 为一代数整数：
此处表明 不是代数整数：
这里给出使 为一代数整数的最小正整数 ：

一个代数数 a 的迹是 MinimalPolynomial[a] 的全体根之和.

这里得到了 的迹：

一个代数数 a 的范数是 MinimalPolynomial[a] 的全体根的乘积.

这里得到了 的范数：

当且仅当 和 均为代数整数，或者等价地，当且仅当 AlgebraicNumberNorm[a] 为 或 时，代数数 是一个代数单位元.

此处表明 GoldenRatio 是一个代数单位元：
此处表明 AlgebraicNumber[Root[#13-4#1+17&,1],{1,2,3}] 不是一个代数单位元：

当且仅当存在一个整数 使得 时，代数数 是一个单位根.

这里表明 是一个单位根：
MinimalPolynomial[s,x,Extension->a]
给出代数数 s 在域 上的特征多项式
MinimalPolynomial[s,x,Extension->Automatic]
给出 AlgebraicNumber 对象 s 在由其第一个参数生成的数域上的特征多项式
AlgebraicNumberTrace[a,Extension->θ]
给出代数数 a 在域 上的迹
AlgebraicNumberTrace[a,Extension->Automatic]
给出 AlgebraicNumber 对象 a 在由其第一个参数生成的数域上的迹
AlgebraicNumberNorm[a,Extension->θ]
给出代数数 a 在域 上的范数
AlgebraicNumberNorm[a,Extension->Automatic]
给出 AlgebraicNumber对象 a 在由其第一个参数生成的数域上的范数

计算代数数域的元素性质的函数.

若 a 为 AlgebraicNumber[θ,coeffs]，则 MinimalPolynomial[a,x,Extension->Automatic] 等于 MinimalPolynomial[a,x]d，其中 d 是 的扩张次数.

由4次有理数扩张的一个元素表示的 的特征多项式等于 的 MinimalPolynomial 的平方：

一个代数数的迹是其特征多项式全体根之和. 如果 a 为 AlgebraicNumber[θ,coeffs]，则AlgebraicNumberTrace[a,Extension->Automatic] 等于 d AlgebraicNumberTrace[a]，其中 d 为 的扩张次数.

以一个4次有理数扩张的一个元素表示的 的迹，是 的 AlgebraicNumberTrace 的两倍：

一个代数数的范数是其特征多项式全体根之积. 如果 a 为 AlgebraicNumber[θ,coeffs]，则 AlgebraicNumberNorm[a,Extension->Automatic] 等于 AlgebraicNumberNorm[a]d，其中 d 为 的扩张次数.

以一个4次有理数扩张的一个元素表示的 的范数是 的AlgebraicNumberNorm 的平方：
NumberFieldIntegralBasis[a]给出由代数数 a 生成的域 的整基（integral basis）
NumberFieldRootsOfUnity[a]给出由代数数 a 生成的域 的单位根
NumberFieldFundamentalUnits[a]给出由代数数 a 生成的域 的一个基本单位列表
NumberFieldNormRepresentatives[a,m]
给出由代数数 a 生成的域 中范式为 ±m 的代数整数类的代表元
NumberFieldSignature[a]给出由代数数 a 生成的域 的标记
NumberFieldDiscriminant[a]给出由代数数 a 生成的域 的判别式
NumberFieldRegulator[a]给出由代数数 a 生成的域 的调节子
NumberFieldClassNumber[a]给出由代数数 a 生成的数域 的类数

计算代数数域性质的函数.

一个代数数域 的整基是一个代数数列表，该列表形成 的代数整数的 ‐模的一个基. 集合 是一个代数数域 的一个整基的充要条件是 为代数整数，并且每一个代数整数 都能够唯一地表示成

其中 为整数系数.

这是 的一个整基：
此处给出由 533+429 #1+18 #12+#13& 的第一个根所生成的域的一个整基：
NumberFieldIntegralBasis 允许通过给出一个多项式和一个根数来对数域进行设定：
这里给出由 Root[9-2 #2+#4&,4] 生成的域的单位根：
这里是域 内的所有单位根：

是一个代数数域 的基本单位列表的充要条件是 为代数单位，并且每个代数单位 都能够被唯一地表示成带有一个单位根 和整数指数 的

的形式.

这里是由 #14-10 #12+1& 的第三个根生成的域的基本单元的集合：
这里给出二次域 的一个基本单元：
这里给出由 #12-7& 生成的域中范数9的元素的类的代表元的集合：
这是域 内范数2的元素的类的代表元的集合：
此处表明多项式 #5+#4+#3+#2+1& 有1个实根和2个复根共轭对：
此处表明域 有12个实数嵌入（real embedding）和6个复数嵌入（complex embedding）共轭对：

一个数域 的判别式是 的一个整基 的判别式（即元素为AlgebraicNumberTrace[ai aj,Extension->Automatic] 的矩阵的行列式式）. 行列式的值与整基的选择无关.

这是 的判别式：
这里给出由多项式 #5+#4+#3+#2+1& 的根生成的域的判别式. 判别式的值与根的选择无关；因此 NumberFieldDiscriminant 允许只对多项式进行设定：

数域 的调节子是 在对数嵌入

下的单位群的像的点格体积，这里 、…、 为 在 上的实数嵌入，、…、 为 在 上复数嵌入的每一个共轭对之一.

这是 的调节子：
这里给出了由多项式 #13-3 #12+1& 的一个根生成的域的调节子. 调节子的值与根的选择无关；因此 NumberFieldRegulator 允许只对多项式进行设定：
这里给出了 的类数：