表达式

万物皆可表达像操作列表一样操作表达式
表达式的意义作为树的表达式
输入表达式的特殊方式表达式的层
表达式的部分
万物皆可表达
Wolfram 语言能够处理各种事物：数学公式、列表、图形，只是其中几个例子. 尽管它们往往看起来有天壤之别，但在Wolfram 语言中，都可以用一种统一的方式表示. 这就是表达式.
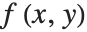
Wolfram 语言表达式的一个典型示例是 f[x,y]. 我们可以使用 f[x,y] 表示数学函数 . 函数名为 f，它具有两个参数 x 和 y.
表达式不必总是写成 f[x,y,…] 的形式. 比如，x+y 也是一个表达式. 当你键入 x+y，Wolfram 语言会将它转换成标准格式 Plus[x,y]. 当它再次输出时，依然会给出 x+y.
其他“运算符”也是如此，例如 ^ (Power) 和 / (Divide).
实际上，在 Wolfram 语言中键入的所有内容都被视为表达式.
x+y+zPlus[x,y,z]
xyzTimes[x,y,z]
x^nPower[x,n]
{a,b,c}List[a,b,c]
a->bRule[a,b]
a=bSet[a,b]
Wolfram 语言表达式的一些示例.
可以使用 FullForm[expr] 来查看任何表达式的完全格式.
这是一个表达式：
这是表达式的完全格式：
这是另一个表达式：
它的完全格式包含几个嵌套：
表达式 f[x,y,…] 中的对象 f 被称为表达式的标头（Head)，可以使用 Head[expr] 提取. 特别是当使用Wolfram 语言编写程序时，您经常会需要测试表达式的标头以具体了解表达式所表示的事物类型.
Head 给出“函数名称” f：
这里，Head 给出“算符”的名称：
一切都有标头：
数值也有标头：
通过标头可以区分不同类型的数值：
Head[expr]
给出表达式的标头：f[x,y] 中的 f
FullForm[expr]
以 Wolfram 语言使用的完全格式显示表达式
用于操作表达式的函数.
表达式的意义
表达式的概念是 Wolfram 系统中一项至关重要的统一原则. 正是因为 Wolfram 系统中的每个对象都具有相同的底层结构，才使得 Wolfram 系统可以用相对较少的基本操作覆盖如此多的应用区域.
所有表达式都具有相同的底层结构，但使用的方式仍可以有多种. 以下是可以对表达式各部分进行的一些解释.
f的意义
x,y,…的意义
例
Function
实参或形参
Sin[x]
,
f[x,y]
命令
实参或形参
Expand[(x+1)^2]
算子
运算数
x+y
,
a=b
Head
元素
{a,b,c}
对象类型
内容
RGBColor[r,g,b]
表达式各部分的一些解释.
Wolfram 系统中的表达式通常用于指定操作. 例如，键入 2+3 会使 2 和 3 相加，而 Factor[x^6-1] 则进行因式分解.
在 Wolfram 系统中，表达式的一个可能更重要的用途是维持结构，然后可以由其他函数进行操作. 像 {a,b,c} 这样的表达式未指定操作. 它仅维持一个由三个元素组成的列表的结构. 其他函数，如 Reverse 或 Dot，可以作用于此结构.
表达式 {a,b,c} 的完全格式是 List[a,b,c]. 标头 List 不执行任何操作. 其目的是用作“标签”以指定结构的“类型”.
在 Wolfram 系统中使用表达式可以创建自己的结构. 例如，您可能想在三维空间中表示由三个坐标指定的点. 可以将每个点用 point[x,y,z] 指定. “函数” point 不执行任何操作. 它仅用于将三个坐标集合在一起，并将所得对象标记为一个 point.
可以将表达式（如 point[x,y,z]）视为用特定标头标记的“数据包”. 即使所有表达式都具有相同的基本结构，也可以通过不同的标头来区分不同的“类型”. 然后可以设置转换规则和程序，以不同的方式处理不同类型的表达式.
输入表达式的特殊方式
在 Wolfram 语言中，许多常见运算符可以使用特殊的符号表示. 例如，尽管在 Wolfram 系统内部，两个项的和表示为 Plus[x,y]，但是输入此表达式时，可以采用更方便的形式 x+y.
Wolfram 语言具有确定的语法来指定应如何将输入转换为内部形式. 该语法一方面指定应如何对输入内容进行分组. 例如，如果输入一个表达式 a+b^c，Wolfram 语言语法指定应按照标准数学符号将其视为 a+(b^c)，而不是 (a+b)^c. Wolfram 语言之所以这样分组，是因为它认为运算符 ^ 的优先级高于 +. 通常，具有较高优先级的运算符的参数先分组，然后具有较低优先级运算符的参数再分组.
应该认识到，Wolfram 语言中的每种特殊输入形式都有明确的优先级. 这不仅包括传统的数学运算符，还包括诸如 ->、:= 之类的形式或用于分隔 Wolfram 语言程序表达式的分号等.
"运算符的输入形式" 的表中按优先级从高到低的顺序给出了 Wolfram 语言的所有运算符. 优先顺序应尽可能遵循标准的数学用法，并尽量减少通常需要的括号个数.
例如，您会发现关系运算符（如 <）的优先级低于算术运算符（如 +）. 这意味着可以在不使用括号的情况下写出 x+y>7 之类的表达式.
但在许多情况下，确实必须使用括号. 例如，因为 ; 优先级比 = 低，写 x=(a;b) 需要使用括号. Wolfram 系统将表达式 x=a;b 解释为 (x=a);b. 通常，括号多余并无大碍，但是如果该加括号而没加，则会造成很多麻烦，Wolfram 系统可能会以不希望的方式来解释您的输入.
f[x,y]
f[x,y] 的标准形式
f@x
f[x] 的前缀形式
x//f
f[x] 的后缀形式
x~f~y
f[x,y] 的中缀形式
Wolfram 语言中表达式的四种写法.
Wolfram 语言中有几种常见的运算符类型. x+y 中的 + 是“中缀”运算符. -p 中的 - 是“前缀”运算符. 即使输入 f[x,y,…] 之类的表达式，Wolfram 语言也允许您模仿中缀、前缀和后缀的形式来写.
此“后缀形式”与 f[x+y] 完全等效：
我们往往会在事后想起添加诸如 N 这样的函数，并以后缀形式给出：
有时将函数写成中缀形式，会更容易理解它的作用：
需要注意的是，// 的优先级很低. 如果把 //f 放到含算术或逻辑运算符的表达式的末尾，f 会作用于整个表达式. 因此，x+y//f 等于 f[x+y]，而不是 x+f[y].
前缀形式 @ 具有更高的优先级. f@x+y 等于 f[x]+y，而不是 f[x+y]. f[x+y] 的前缀形式可以写作 f@(x+y).
表达式的部分
由于列表只是一种特殊形式的表达式，自然我们可以像指代列表的一部分一样指代表达式的一部分.
这将获得列表 {a,b,c} 中的第二个元素：
可以使用相同的方法得到 x+y+z 总和中的第二个元素：
给出和式的最后一个元素：
部分 0 为表达式的标头：
可以指代表达式的某些部分（例如 f[g[a],g[b]]）就像指代嵌套列表的部分一样.
这是部分 1：
这是部分 {1,1}：
提取表达式 1+x^2 的部分 {2,1}：
如要了解部分 {2,1} 的内容，可以查看表达式的完全格式：
应该认识到，将指标分配给表达式的各部分是根据表达式的内部 Wolfram 语言形式完成的，如 FullForm 所示. 这些形式并不总与输出内容直接对应. 代数表达式尤其如此，其中 Wolfram 语言使用标准内部形式，但以特殊方式显示表达式.
这是 x/y 的内部形式：
内部形式用于指定部分：
可以像操作列表的一部分一样，操作表达式的一部分.
这里用 x^2 代替 a+b+c+d 的第三部分. 注意，替换完成后，总和会自动重新排列：
这是一个表达式：
这是 t 的完全格式：
这将重置表达式 t 的一部分：
现在，t 的形式已经改变：
Part[expr,n]
or
expr[[n]]
expr 的第 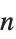部分
Part[expr,{n1,n2,…}]
or
expr[[{n1,n2,…}]]
表达式各部分的组合
Part[expr,n1;;n2]
表达式的 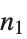至 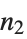部分
ReplacePart[expr,n->elem]
用 elem 代替 expr 的第 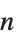部分
用于操作表达式部分的函数.
"操作列表元素" 讨论如何使用指标列表一次选择列表中的几个元素. 可以使用相同的方式一次选择表达式的多个部分.
这将选择列表中的第2和4个元素，并给出这些元素的列表：
这将选择和式中的第2和4个部分，并给出这些元素的和：
表达式中的任何部分都可以视为某个函数的参数. 当通过提供指标列表来选取多个部分时，这些部分将使用与表达式中相同的函数进行组合.
这将挑选出列表的第2至第4个部分：
像操作列表一样操作表达式
"列表"中介绍的大部分列表操作都可以用于 Wolfram 语言表达式. 通过这些操作，从而用多种方式来操纵表达式的结构.
这个表达式与各项总和相对应：
Take[t,2] 取 t 的前两个元素，就像 t 是一个列表一样：
Length 给出 t 中元素的个数：
可以使用 FreeQ[expr,form] 测试 form 是否不在 expr 中出现：
给出 x 在 t 中出现的位置的列表：
应该记住，所有操纵表达式结构的函数都作用于表达式的内部形式. 可以使用 FullForm[expr] 查看这些形式. 它们可能不是所期望的表达式输出格式.
这是带有四个参数的函数：
可以使用 Append 添加参数：
将参数次序颠倒：
如“结构操作”中所述，还有一些其他函数可以与表达式一起使用.
作为树的表达式
这是一个表达式的完全格式：
TreeForm 打印出表达式以显示其“树”结构：
任何 Wolfram 语言表达式都可以被看成树. 在上面的表达式中，树的顶部节点由 Plus 组成. 从该节点进入两个“分支”，x^3 和 (1+x)^2. 节点 x^3 上有两个分支 x 和 3，它们可以看作树的“叶子”.
该矩阵是一个只有两层的简单树：
这是一个更复杂的表达式：
这个表达式的树有很多层：
标记表达式各部分的指标对树有简单的解释. 从树的顶部节点向下，每个指标指定要到达所需部分的分支.
表达式的层
通过函数 Part 可以访问 Wolfram 语言表达式的特定部分. 但是当表达式具有相当统一的结构时，能够同时指代部分的一整组集合通常更方便.
层提供了一种在 Wolfram 语言表达式中指定部分集合的通用方法. 许多 Wolfram 语言函数允许在表达式中指定应作用的层.
这是一个简单的表达式，以树形式显示：
这将在表达式 t 的第1层中搜索 x. 仅找到一次：
这将搜索至第2层. 现在 x 的两个位置都找到了：
这将仅在第2层搜索. x 仅出现一次：
Position[expr,form,n]
给出 form 在 expr 中 n 层以下所出现的位置
Position[expr,form,{n}]
给出在 n 层出现的位置
使用层控制 Position.
可以把表达式中的层当成树. 表达式中特定部分的层是该部分出现在树上的距离，树的顶部位于第0层.
也可以说，出现在第 n 层的部分是正好可以由 n 个指标序列指定的部分.
n
第 1 至 n 层
Infinity
所有层（0除外）
{n}
仅第 n 层
{n1,n2}
第 n1 至 n2 层
Heads->True
包括标头
Heads->False
标头除外
层的规范.
这是一个表达式，以树形式显示：
从第2层向下搜索 a：
这显示了 f 在表达式的标头之外出现的位置：
这里包括了 f 在表达式标头中的出现情况：
Level[expr,lev]
expr 中由 lev 指定的层的部分列表
Depth[expr]
expr 中的总层数
测试和提取层.
这给出了 u 的第2层以下所有部分的列表：
Here are the parts specifically at level 2:
在掌握了普通的层的概念，现在来考虑负层. 负级标记的部分表达式从树的底部开始. 层-1包含树的所有叶子：符号和数字之类的对象.
这里显示 u 在层-1的部分：
可以认为表达式具有“深度”，如 TreeForm 所示. 通常，表达式的层 -n 定义为由深度为 n 的所有子表达式组成.
g[a] 的深度为2：
u 在-2层的部分是那些深度恰好为2的部分：