Element

Element[x,dom]

or x∈dom asserts that x is an element of the domain dom.

Element[x,reg]

or x∈reg asserts that x is an element of the region reg.

Element[x1|x2|…,dom]

asserts that all the xi are elements of dom.

Element[patt,dom]

asserts that any expression matching the pattern patt is an element of dom.

Details

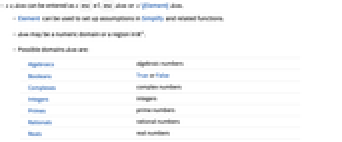
  • x∈dom can be entered as x el dom or x \[Element] dom.
  • Element can be used to set up assumptions in Simplify and related functions.
  • dom may be a numeric domain or a region in .
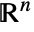  • Possible domains dom are:
  • Algebraicsalgebraic numbers
    BooleansTrue or False
    Complexescomplex numbers
    Integersintegers
    Primesprime numbers
    Rationalsrational numbers
    Realsreal numbers
  • Possible regions reg are defined by RegionQ.
  • x∈dom if possible evaluates immediately when x is numeric.
  • For a domain dom, {x1,x2,…}∈dom is equivalent to (x1|x2|…)∈dom.
  • For a region reg, {x1,x2,…}∈reg asserts that the point with coordinates x1,x2,… belongs to reg.
  • {x1,x2,…}∈dom evaluates to (x1|x2|…)∈dom if its truth or falsity cannot immediately be determined.

Examples

open allclose all

Basic Examples  (5)

Test whether is an element of the reals:

Test whether the point belongs to the unit disk:

Express domain membership for an expression:

Assert that the point belongs to the unit ball:

Use element assertions to integrate over a region:

Or to optimize over a region:

Enter using elem:

Scope  (9)

Test domain membership:

Test region membership:

Plot it:

Make domain membership assumptions:

Express region membership:

Test domain membership using assumptions:

Test region membership using assumptions:

Specify variable domains:

Specify assumptions on objects matching a pattern:

TraditionalForm formatting:

Properties & Relations  (2)

For a single variable, the negation of Element is automatically converted to NotElement:

For multiple variables, the negation of Element is not automatically simplified:

Use LogicalExpand to find the representation in terms of NotElement:

Element asserts region membership:

RegionMember gives explicit region membership conditions:

Possible Issues  (1)

When domain membership cannot be decided the Element statement remains unevaluated:

Wolfram Research (1999), Element, Wolfram Language function, https://reference.wolfram.com/language/ref/Element.html (updated 2014).

Text

Wolfram Research (1999), Element, Wolfram Language function, https://reference.wolfram.com/language/ref/Element.html (updated 2014).

CMS

Wolfram Language. 1999. "Element." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/Element.html.

APA

Wolfram Language. (1999). Element. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Element.html

BibTeX

@misc{reference.wolfram_2024_element, author="Wolfram Research", title="{Element}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/Element.html}", note=[Accessed: 25-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_element, organization={Wolfram Research}, title={Element}, year={2014}, url={https://reference.wolfram.com/language/ref/Element.html}, note=[Accessed: 25-December-2024 ]}