finds the pseudoinverse of a rectangular matrix.


PseudoInverse
finds the pseudoinverse of a rectangular matrix.
Details and Options

- PseudoInverse works on both symbolic and numerical matrices.
- For a square matrix, PseudoInverse gives the Moore–Penrose inverse.
- For numerical matrices, PseudoInverse is based on SingularValueDecomposition.
- PseudoInverse[m,Tolerance->t] specifies that singular values smaller than t times the maximum singular value should be dropped.
- With the default setting Tolerance->Automatic, singular values are dropped when they are less than 100 times 10-p, where p is Precision[m].
- For nonsingular square matrices M, the pseudoinverse
![TemplateBox[{M}, PseudoInverse] TemplateBox[{M}, PseudoInverse]](Files/PseudoInverse.en/1.png) is equivalent to the standard inverse
is equivalent to the standard inverse ![TemplateBox[{M}, Inverse] TemplateBox[{M}, Inverse]](Files/PseudoInverse.en/2.png) .
. - PseudoInverse[m] formats as
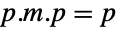 in StandardForm and TraditionalForm. »
in StandardForm and TraditionalForm. »
Examples
open all close allBasic Examples (5)
Find the pseudoinverse of an invertible matrix:
The pseudoinverse is merely the inverse:
Find the pseudoinverse of a singular matrix:
The determinant of ![]() is zero, so it does not have a true inverse:
is zero, so it does not have a true inverse:
For a pseudoinverse, both ![]() and
and ![]() :
:
However, in this particular case neither ![]() nor
nor ![]() is an identity matrix:
is an identity matrix:
Find the pseudoinverse of a rectangular matrix:
In this particular case, ![]() is an identity matrix:
is an identity matrix:
Scope (11)
Basic Uses (7)
Special Matrices (4)
The pseudoinverse of a sparse matrix is returned as a normal matrix:
When possible, the pseudoinverse of a structured matrix is returned as another structured matrix:
IdentityMatrix[n] is its own pseudoinverse:
The pseudoinverse of IdentityMatrix[{m,n}] is a transposition:
Compute the pseudoinverse for HilbertMatrix:
Options (1)
Tolerance (1)
Some singular values are below the default tolerance for machine precision:
Compute the pseudoinverse with the default tolerance:
It is not a true inverse since some singular values were considered to be effectively zero:
Compute the pseudoinverse with no tolerance:
Even though no singular values were considered zero, it is worse due to numerical error:
Applications (8)
Equation Solving (4)
Solve the following system of equations using PseudoInverse:
Rewrite the system in matrix form:
The general solution is given by ![]() for an arbitrary vector
for an arbitrary vector ![]() :
:
Since the ![]() dropped out, the solution is unique, as can be verified using SolveValues:
dropped out, the solution is unique, as can be verified using SolveValues:
Find all solutions of the following system of equations:
First, write the coefficient matrix ![]() , vector variable
, vector variable ![]() and constant vector
and constant vector ![]() :
:
The general solution is given by ![]() for an arbitrary vector
for an arbitrary vector ![]() :
:
Although there are three parameters, this solution represents a line:
This is because the null space of ![]() is one-dimensional:
is one-dimensional:
Hence it is possible to reparameterize to eliminate two of the parameters:
This parameterization gives the answer in the same form as SolveValues:
Find the minimum Frobenius-norm solution to ![]() , with
, with ![]() and
and ![]() as follows:
as follows:
The minimum norm solution is ![]() :
:
Compute the Frobenius norm of ![]() :
:
As in the vector case, the general solution is given by ![]() , with
, with ![]() now an arbitrary matrix:
now an arbitrary matrix:
The minimum occurs when all the ![]() are zero, confirming that
are zero, confirming that ![]() is the minimum-norm solution:
is the minimum-norm solution:
In this case there is no solution to ![]() :
:
An approximate solution that minimizes the norm of ![]() is given by
is given by ![]() :
:
Compare to general minimization:
A more general solution is given by ![]() :
:
Although there are three parameters in ![]() , it represents a line:
, it represents a line:
Least Squares and Curve Fitting (4)
For the matrix ![]() and vector
and vector ![]() that follow, find a vector
that follow, find a vector ![]() that minimizes
that minimizes ![]() :
:
One solution, in this case unique, is given by ![]() :
:
This result could also have been obtained using LeastSquares[m,b]:
Confirm the answer using Minimize:
For the matrices ![]() and
and ![]() that follow, find a matrix
that follow, find a matrix ![]() that minimizes
that minimizes ![]() :
:
One solution, in this case unique, is given by ![]() :
:
This result could also have been obtained using LeastSquares[m,b]:
Confirm the answer using Minimize:
PseudoInverse can be used to find a best-fit curve to data. Consider the following data:
Extract the ![]() and
and ![]() coordinates from the data:
coordinates from the data:
Construct a design matrix, whose columns are ![]() and
and ![]() , for fitting to a line
, for fitting to a line ![]() :
:
Get the coefficients ![]() and
and ![]() for a linear least‐squares fit:
for a linear least‐squares fit:
Verify the coefficients using Fit:
Plot the best-fit curve along with the data:
Find the best-fit parabola to the following data:
Extract the ![]() and
and ![]() coordinates from the data:
coordinates from the data:
Construct a design matrix, whose columns are ![]() ,
, ![]() and
and ![]() , for fitting to a line
, for fitting to a line ![]() :
:
Get the coefficients ![]() ,
, ![]() and
and ![]() for a least‐squares fit:
for a least‐squares fit:
Verify the coefficients using Fit:
Properties & Relations (14)
For a nonsingular matrix, the pseudoinverse is the same as the inverse:
PseudoInverse is involutive, ![]() :
:
PseudoInverse commutes with Transpose, i.e ![]() :
:
It also commutes with Conjugate, ![]() :
:
Hence it commutes with ConjugateTranspose, ![]() :
:
PseudoInverse satisfies the Moore–Penrose equations [more info]:
If MatrixRank[m] equals the number of columns of ![]() , then
, then ![]() :
:
In particular, PseudoInverse[m] is a left-inverse of m:
If MatrixRank[m] equals the number of rows of ![]() , then
, then ![]() :
:
In particular, PseudoInverse[m] is a right-inverse of m:
For a diagonal matrix d, PseudoInverse[d] is the transpose with nonzero elements inverted:
If ![]() has the singular value decomposition
has the singular value decomposition ![]() , then
, then ![]() :
:
If a is an ![]() matrix and MatrixRank[a]==m, QRDecomposition will give the pseudoinverse:
matrix and MatrixRank[a]==m, QRDecomposition will give the pseudoinverse:
A normal matrix ![]() commutes with its pseudoinverse:
commutes with its pseudoinverse:
PseudoInverse[m] can be computed as ![]() , where
, where ![]() denotes DrazinInverse:
denotes DrazinInverse:
LeastSquares and PseudoInverse can both be used to solve the least-squares problem:
![]() gives the minimum norm
gives the minimum norm ![]() that minimizes the residual
that minimizes the residual ![]() :
:
Verify that ![]() minimizes the residual:
minimizes the residual:
Adding any vector in the NullSpace of ![]() to
to ![]() will leave the residual unchanged:
will leave the residual unchanged:
The minimum norm ![]() occurs at
occurs at ![]() , i.e when
, i.e when ![]() :
:
For a vector ![]() and a matrix
and a matrix ![]() with empty nullspace,
with empty nullspace, ![]() equals ArgMin[Norm[m.x-b],x]:
equals ArgMin[Norm[m.x-b],x]:
See Also
Inverse LeastSquares Fit SingularValueDecomposition SingularValueList DrazinInverse
Function Repository: ProjectionMatrix
Tech Notes
Related Links
History
Introduced in 1988 (1.0) | Updated in 2003 (5.0) ▪ 2025 (14.3)
Text
Wolfram Research (1988), PseudoInverse, Wolfram Language function, https://reference.wolfram.com/language/ref/PseudoInverse.html (updated 2025).
CMS
Wolfram Language. 1988. "PseudoInverse." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/PseudoInverse.html.
APA
Wolfram Language. (1988). PseudoInverse. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PseudoInverse.html
BibTeX
@misc{reference.wolfram_2025_pseudoinverse, author="Wolfram Research", title="{PseudoInverse}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/PseudoInverse.html}", note=[Accessed: 23-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_pseudoinverse, organization={Wolfram Research}, title={PseudoInverse}, year={2025}, url={https://reference.wolfram.com/language/ref/PseudoInverse.html}, note=[Accessed: 23-January-2026]}