HyperexponentialDistribution[{α1,…,αm},{λ1,…,λm}]
represents an m-phase hyperexponential distribution with phase probabilities αi and rates λi.


HyperexponentialDistribution
HyperexponentialDistribution[{α1,…,αm},{λ1,…,λm}]
represents an m-phase hyperexponential distribution with phase probabilities αi and rates λi.
Details

- HyperexponentialDistribution is also known as a mixed exponential or parallel m-phase exponential distribution.
- An m-phase hyperexponential distribution can be interpreted as having m servers in parallel where the i
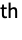 server has service rate λi and is picked with probability αi.
server has service rate λi and is picked with probability αi. - The probability density for value
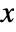 in an exponential distribution is
in an exponential distribution is 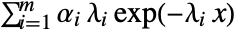 for
for 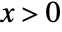 , and is zero for
, and is zero for 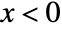 .
. - HyperexponentialDistribution allows αi to be any non-negative numbers such that α1+⋯+αm1 and λi can be any positive real numbers.
- HyperexponentialDistribution allows λi to be any quantities of the same unit dimensions and αi to be dimensionless quantities. »
- HyperexponentialDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- HyperexponentialDistribution[{α1,…,αm},{λ1,…,λm}] represents a continuous statistical distribution defined over the interval
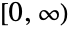 , parameterized by two vectors (α1,…,αm) and (λ1,…,λm), and known as an
, parameterized by two vectors (α1,…,αm) and (λ1,…,λm), and known as an 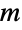 -phase hyperexponential distribution. The parameters αi are called "phase probabilities", have values in the interval
-phase hyperexponential distribution. The parameters αi are called "phase probabilities", have values in the interval 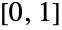 , and satisfy
, and satisfy 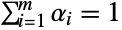 , while the parameters λi are called "phase rates" and have positive real values. Together these parameters determine the overall shape of the probability density function (PDF), which in general is monotonic decreasing and has tails that are "thin" in the sense that the PDF decreases exponentially rather than algebraically for large values of
, while the parameters λi are called "phase rates" and have positive real values. Together these parameters determine the overall shape of the probability density function (PDF), which in general is monotonic decreasing and has tails that are "thin" in the sense that the PDF decreases exponentially rather than algebraically for large values of 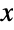 . (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) Random variables
. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) Random variables 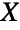 satisfying XHyperexponentialDistribution[{α1,…,αm},{λ1,…,λm}] are sometimes said to have a hyperexponential distribution of order
satisfying XHyperexponentialDistribution[{α1,…,αm},{λ1,…,λm}] are sometimes said to have a hyperexponential distribution of order 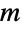 .
. - Named because its coefficient of variation (the ratio of StandardDeviation to Mean) is always larger than 1 (which is the coefficient of variation for any exponential distribution), the hyperexponential distribution is an example of a mixture distribution and is often thought of as a generalization of ExponentialDistribution in the sense that its PDF is the sum of exponential density functions. Because it has thin tails, the hyperexponential distribution is an often-used model for studying queueing systems and sensor networks. One unique property of the hyperexponential distribution is that it can be used to approximate arbitrary probability distributions (even those with heavy tails), a fact that is used in the study of network performance models to capture performance data for various queueing models that cannot be quantitatively deduced using exact methods. The hyperexponential distribution has also been used in the study of semiconductors, manufacturing systems, and computer hardware architecture.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a hyperexponential distribution. Distributed[x,HyperexponentialDistribution[{α1,…,αm},{λ1,…,λm}]], written more concisely as xHyperexponentialDistribution[{α1,…,αm},{λ1,…,λm}], can be used to assert that a random variable x is distributed according to a hyperexponential distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[HyperexponentialDistribution[{α1,…,αm},{λ1,…,λm}],x] and CDF[HyperexponentialDistribution[{α1,…,αm},{λ1,…,λm}],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a hyperexponential distribution, EstimatedDistribution to estimate a hyperexponential parametric distribution from given data, and FindDistributionParameters to fit data to a hyperexponential distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic hyperexponential distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic hyperexponential distribution.
- TransformedDistribution can be used to represent a transformed hyperexponential distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a hyperexponential distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving hyperexponential distributions.
- The hyperexponential distribution is related to a number of other distributions. HyperexponentialDistribution is an obvious generalization of ExponentialDistribution in that an exponential distribution ExponentialDistribution[λ1] can be viewed both as a single-phase hyperexponential HyperexponentialDistribution[{1},{λ1}] and as a hyperexponential HyperexponentialDistribution[{α1,α2,…,αm},{λ1,λ1,…,λ1}] in which the phase rates λ1 are all equal. HyperexponentialDistribution can also be realized as a mixture distribution whose weights are each ExponentialDistribution. In addition, HyperexponentialDistribution can be transformed into HypoexponentialDistribution (and vice versa); can be obtained from GammaDistribution, LaplaceDistribution, BenktanderWeibullDistribution, LogisticDistribution, ParetoDistribution, PearsonDistribution, PowerDistribution, and RayleighDistribution by composing transformations of ExponentialDistribution with TransformedDistribution and/or TruncatedDistribution; and is related to CoxianDistribution, ExtremeValueDistribution, GumbelDistribution, FrechetDistribution, and WeibullDistribution, among others.
Examples
open all close allBasic Examples (4)
Scope (8)
Generate a sample of pseudorandom numbers from a hyperexponential distribution:
Compare the histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare a density histogram of the sample with the PDF of the estimated distribution:
When both rates go to ![]() simultaneously:
simultaneously:
When both rates go to 0 simultaneously:
When both rates go to ![]() simultaneously:
simultaneously:
When both rates go to 0 simultaneously:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Closed form for symbolic order:
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (1)
Suppose a customer is buying an appliance and is choosing at random between an appliance with an average lifetime of 10 years and an appliance with an average lifetime of 12 years. Assuming the lifetime of this appliance follows an exponential distribution, find the lifetime distribution of the purchased appliance:
Find the probability that the appliance will work for more than 15 years:
Properties & Relations (6)
The variation coefficient of the hyperexponential distribution is always greater than the variation coefficient of ExponentialDistribution:
There are no valid parameters such that the variation coefficient of the hyperexponential distribution is less than or equal to the variation coefficient of an exponential distribution:
Hyperexponential distribution is closed under scaling by a positive factor:
Relationships to other distributions:
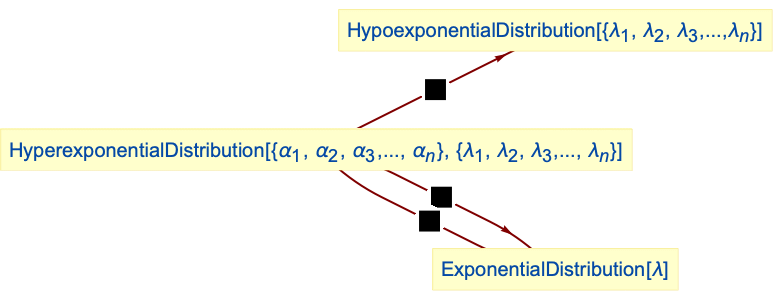
Hyperexponential distribution with a single phase is ExponentialDistribution:
Hyperexponential distribution with equal phase probabilities is ExponentialDistribution:
Related Guides
Text
Wolfram Research (2012), HyperexponentialDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/HyperexponentialDistribution.html (updated 2016).
CMS
Wolfram Language. 2012. "HyperexponentialDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/HyperexponentialDistribution.html.
APA
Wolfram Language. (2012). HyperexponentialDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HyperexponentialDistribution.html
BibTeX
@misc{reference.wolfram_2025_hyperexponentialdistribution, author="Wolfram Research", title="{HyperexponentialDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/HyperexponentialDistribution.html}", note=[Accessed: 25-November-2025]}
BibLaTeX
@online{reference.wolfram_2025_hyperexponentialdistribution, organization={Wolfram Research}, title={HyperexponentialDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/HyperexponentialDistribution.html}, note=[Accessed: 25-November-2025]}