Mathematical and Other Notation
Mathematical and Other Notation
If you use a text‐based interface to the Wolfram Language, then the input you give must consist only of characters that you can type directly on your computer keyboard. But if you use a notebook interface then other kinds of input become possible.
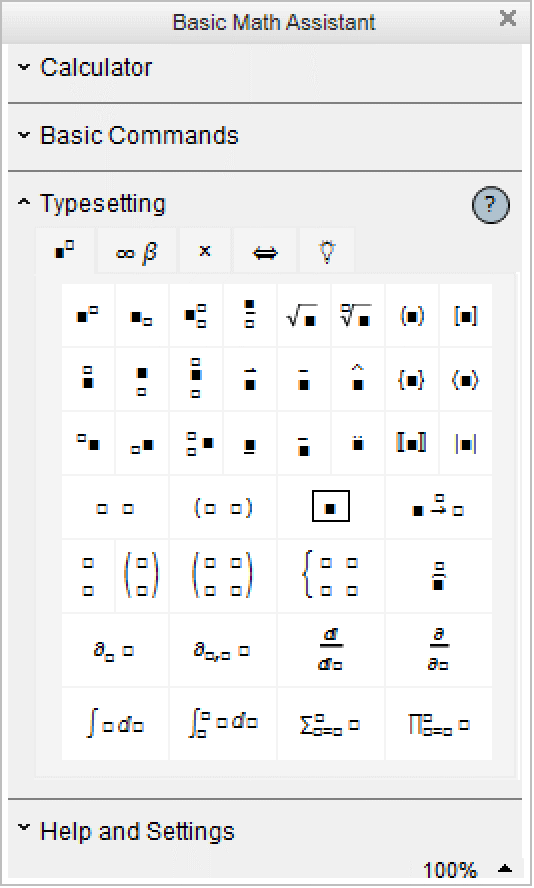
There are palettes provided which operate like extensions of your keyboard, and which have buttons that you can click to enter particular forms. You can access standard palettes using the Palettes menu.
Clicking the first button in this palette will create an empty structure for entering a power. You can use the mouse to fill in the structure.
You can also give input by using special keys on your keyboard. Pressing one of these keys does not lead to an ordinary character being entered, but instead typically causes some action to occur or some structure to be created.
Esc
p
Esc
| the symbol |
Esc
inf
Esc
| the symbol |
Esc
ee
Esc
| |
Esc
ii
Esc
| |
Esc
deg
Esc
| |
Ctrl+^ or Ctrl+6 | go to the superscript for a power |
Ctrl
+
/
| go to the denominator for a fraction |
Ctrl+@ or Ctrl+2 | go into a square root |
Ctrl
+
Space
|
return from a superscript, denominator or square root
|
In a traditional computer language such as C, Fortran, Java, or Perl, the input you give must always consist of a string of ordinary characters that can be typed directly on a keyboard. But the Wolfram Language also allows you to give input that contains special characters, superscripts, built‐up fractions, and so on.
The language incorporates many features of traditional mathematical notation. But you should realize that the goal of the language is to provide a precise and consistent way to specify computations. And as a result, it does not follow all of the somewhat haphazard details of traditional mathematical notation.
Nevertheless, as discussed in "Forms of Input and Output", it is always possible to get the Wolfram Language to produce output that imitates every aspect of traditional mathematical notation. And it is also possible for the Wolfram Language to import text that uses such notation, and to some extent to translate it into its own more precise language.
Built into the Wolfram Language are a large number of special characters intended for use in mathematical and other notation. "Listing of Named Characters" gives a complete listing.
Each special character is assigned a full name such as \[Infinity]. More common special characters are also assigned aliases, such as EscinfEsc. You can set up additional aliases using the InputAliases notebook option discussed in "Options for Expression Input and Output".
For special characters that are supported in standard dialects of TeX, the Wolfram Language also allows you to use aliases based on TeX names. Thus, for example, you can enter \[Infinity] using the alias Esc\inftyEsc. The Wolfram Language also supports aliases such as Esc∞Esc based on names used in SGML and HTML.
Standard system software on many computer systems also supports special key combinations for entering certain special characters. On a Macintosh, for example, Option+5 will produce  in most fonts. With the notebook front end the Wolfram System automatically allows you to use special key combinations when these are available, and with a text‐based interface you can get the Wolfram System to accept such key combinations if you set an appropriate value for $CharacterEncoding.
in most fonts. With the notebook front end the Wolfram System automatically allows you to use special key combinations when these are available, and with a text‐based interface you can get the Wolfram System to accept such key combinations if you set an appropriate value for $CharacterEncoding.
■ Use a full name such as \[Infinity] |
■ Use an alias such as EscinfEsc |
■ Use a TeX alias such as Esc\inftyEsc |
■ Use an SGML or HTML alias such as Esc∞Esc |
■ Click a button in a palette |
■ Use a special key combination supported by your computer system |
In a Wolfram System notebook, you can use special characters just like you use standard keyboard characters. You can include special characters both in ordinary text and in input that you intend to give to the Wolfram System.
Some special characters are set up to have an immediate meaning to the Wolfram System. Thus, for example,  is taken to be the symbol Pi. Similarly,
is taken to be the symbol Pi. Similarly,  is taken to be the operator >=, while
is taken to be the operator >=, while  is equivalent to the function Union.
is equivalent to the function Union.
Among ordinary characters such as E and i, some have an immediate meaning to the Wolfram System, but most do not. And the same is true of special characters.
Characters such as 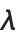 and
and 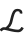 are treated by the Wolfram System as letters—just like ordinary keyboard letters like a or b.
are treated by the Wolfram System as letters—just like ordinary keyboard letters like a or b.
But characters such as  and
and  are treated by the Wolfram System as operators. And although these particular characters are not assigned any built‐in meaning by the Wolfram System, they are nevertheless required to follow a definite syntax.
are treated by the Wolfram System as operators. And although these particular characters are not assigned any built‐in meaning by the Wolfram System, they are nevertheless required to follow a definite syntax.
The details of how input you give to the Wolfram System is interpreted depends on whether you are using StandardForm or TraditionalForm, and on what additional information you supply in InterpretationBox and similar constructs.
But unless you explicitly override its built‐in rules by giving your own definitions for MakeExpression, the Wolfram System will always assign the same basic syntactic properties to any particular special character.
These properties not only affect the interpretation of the special characters in Wolfram System input, but also determine the structure of expressions built with these special characters. They also affect various aspects of formatting; operators, for example, have extra space left around them, while letters do not.
In using special characters, it is important to make sure that you have the correct character for a particular purpose. There are quite a few examples of characters that look similar, yet are in fact quite different.
A common issue is operators whose forms are derived from letters. An example is  or \[Sum], which looks very similar to
or \[Sum], which looks very similar to  or \[CapitalSigma].
or \[CapitalSigma].
As is typical, however, the operator form  is slightly less elaborate and more stylized than the letter form
is slightly less elaborate and more stylized than the letter form  . In addition,
. In addition,  is an extensible character that grows depending on the summand, while
is an extensible character that grows depending on the summand, while  has a size determined only by the current font.
has a size determined only by the current font.
In cases such as \[CapitalAlpha] versus A, both characters are letters. However, the Wolfram System treats these characters as different, and in some fonts, for example, they may look quite different.
Traditional mathematical notation occasionally uses ordinary letters as operators. An example is the d in a differential such as dx that appears in an integral.
To make the Wolfram System have a precise and consistent syntax, it is necessary at least in StandardForm to distinguish between an ordinary d and the 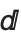 used as a differential operator.
used as a differential operator.
The way the Wolfram System does this is to use a special character 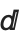 or \[DifferentialD] as the differential operator. This special character can be entered using the alias EscddEsc.
or \[DifferentialD] as the differential operator. This special character can be entered using the alias EscddEsc.
The Wolfram System uses a special character for the differential operator, so there is no conflict with an ordinary d:
When letters and letter‐like forms appear in Wolfram System input, they are typically treated as names of symbols. But when operators appear, functions must be constructed that correspond to these operators. In almost all cases, what the Wolfram System does is to create a function whose name is the full name of the special character that appears as the operator.
The Wolfram System constructs a CirclePlus function to correspond to the operator  , whose full name is ∖[CirclePlus]:
, whose full name is ∖[CirclePlus]:
This constructs an And function, which happens to have built‐in evaluation rules in the Wolfram System:
Following the correspondence between operator names and function names, special characters such as  that represent built‐in Wolfram System functions have names that correspond to those functions. Thus, for example,
that represent built‐in Wolfram System functions have names that correspond to those functions. Thus, for example, 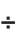 is named \[Divide] to correspond to the built‐in Wolfram System function Divide, and
is named \[Divide] to correspond to the built‐in Wolfram System function Divide, and  is named \[Implies] to correspond to the built‐in function Implies.
is named \[Implies] to correspond to the built‐in function Implies.
In general, however, special characters in the Wolfram Language are given names that are as generic as possible, so as not to prejudice different uses. Most often, characters are thus named mainly according to their appearance. The character  is therefore named \[CirclePlus], rather than, say \[DirectSum], and
is therefore named \[CirclePlus], rather than, say \[DirectSum], and 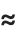 is named \[TildeTilde] rather than, say, \[ApproximatelyEqual].
is named \[TildeTilde] rather than, say, \[ApproximatelyEqual].
There are sometimes characters that look similar but that are used to represent different operators. An example is \[Times] and \[Cross]. \[Times] corresponds to the ordinary Times function for multiplication; \[Cross] corresponds to the Cross function for vector cross products. The  for \[Cross] is drawn slightly smaller than
for \[Cross] is drawn slightly smaller than  for \[Times], corresponding to usual careful usage in mathematical typography.
for \[Times], corresponding to usual careful usage in mathematical typography.
The \[Times] operator represents ordinary multiplication:
The \[Cross] operator represents vector cross products:
In the example of \[And] and \[Wedge], the \[And] operator—which happens to be drawn slightly larger—corresponds to the built‐in Wolfram System function And, while the \[Wedge] operator has a generic name based on the appearance of the character and has no built‐in meaning.
Some of the special characters commonly used as operators in mathematical notation look similar to ordinary keyboard characters. Thus, for example, 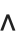 or ∖[Wedge] looks similar to the ^ character on a standard keyboard.
or ∖[Wedge] looks similar to the ^ character on a standard keyboard.
The Wolfram System interprets a raw ^ as a power. But it interprets 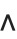 as a generic Wedge function. In cases such as this where there is a special character that looks similar to an ordinary keyboard character, the convention is to use the ordinary keyboard character as the alias for the special character. Thus, for example, Esc^Esc is the alias for \[Wedge].
as a generic Wedge function. In cases such as this where there is a special character that looks similar to an ordinary keyboard character, the convention is to use the ordinary keyboard character as the alias for the special character. Thus, for example, Esc^Esc is the alias for \[Wedge].
A related convention is that when a special character is used to represent an operator that can be typed using ordinary keyboard characters, those characters are used in the alias for the special character. Thus, for example, Esc->Esc is the alias for  or \[Rule], while Esc&&Esc is the alias for
or \[Rule], while Esc&&Esc is the alias for  or \[And].
or \[And].
form | character name | alias | interpretation |
| x|y | | | Alternatives[x,y] | |
| xy | \[VerticalSeparator] | Esc|Esc | VerticalSeparator[x,y] |
| xy | \[VerticalBar] | Esc␣|Esc | VerticalBar[x,y] |
| x | \[LeftBracketingBar] | Escl|Esc | BracketingBar[x] |
| \[RightBracketingBar] | Escr|Esc |
Notice that the alias for \[VerticalBar] is Esc␣|Esc, while the alias for the somewhat more common \[VerticalSeparator] is Esc|Esc. The Wolfram Language often gives similar‐looking characters similar aliases; it is a general convention that the aliases for the less commonly used characters are distinguished by having spaces at the beginning.
| EscnnnEsc | built‐in alias for a common character |
| Esc␣nnnEsc | built‐in alias for similar but less common character |
| Esc.nnnEsc | alias globally defined in a Wolfram System session |
| Esc,nnnEsc | alias defined in a specific notebook |
The notebook front end for the Wolfram System often allows you to set up your own aliases for special characters. If you want to, you can overwrite the built‐in aliases. But the convention is to use aliases that begin with a dot or comma.
Note that whatever aliases you may use to enter special characters, the full names of the characters will always be used when the characters are stored in files.
The Wolfram Language by default interprets any sequence of letters or letter‐like forms as the name of a symbol.
form | character name | alias | interpretation |
| \[Pi] |
Esc
p
Esc
,
Esc
pi
Esc
| equivalent to Pi | |
| \[Infinity] |
Esc
inf
Esc
| equivalent to Infinity | |
| \[ExponentialE] |
Esc
ee
Esc
| equivalent to E | |
| \[ImaginaryI] |
Esc
ii
Esc
| equivalent to I | |
| \[ImaginaryJ] |
Esc
jj
Esc
| equivalent to I |
Essentially all symbols with built‐in meanings in the Wolfram Language have names that start with capital English letters. Among the exceptions are 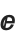 and
and  , which correspond to E and I respectively.
, which correspond to E and I respectively.
In written material, it is standard to use very short names—often single letters—for most of the mathematical objects that one considers. But in the Wolfram Language, it is usually better to use longer and more explicit names.
In written material you can always explain that a particular single‐letter name means one thing in one place and another in another place. But in the Wolfram Language, unless you use different contexts, a global symbol with a particular name will always be assumed to mean the same thing.
As a result, it is typically better to use longer names, which are more likely to be unique, and which describe more explicitly what they mean.
For variables to which no value will be assigned, or for local symbols, it is nevertheless convenient and appropriate to use short, often single‐letter, names.
It is sensible to give the global function LagrangianL a long and explicit name. The local variables can be given short names:
form | input | interpretation |
| xn | x Ctrl+_ n Ctrl+Space | Subscript[x,n] |
| x+ | x Ctrl+_ + Ctrl+Space | SubPlus[x] |
| x- | x Ctrl+_ - Ctrl+Space | SubMinus[x] |
| x* | x Ctrl+_ * Ctrl+Space | SubStar[x] |
| x+ | x Ctrl+^ + Ctrl+Space | SuperPlus[x] |
| x- | x Ctrl+^ - Ctrl+Space | SuperMinus[x] |
| x* | x Ctrl+^ * Ctrl+Space | SuperStar[x] |
| x† | x Ctrl+^ EscdgEsc Ctrl+Space | SuperDagger[x] |
x Ctrl+& _ Ctrl+Space | OverBar[x] | |
x Ctrl+& EscvecEsc Ctrl+Space | OverVector[x] | |
x Ctrl+& ~ Ctrl+Space | OverTilde[x] | |
x Ctrl+& ^ Ctrl+Space | OverHat[x] | |
x Ctrl+& . Ctrl+Space | OverDot[x] | |
x Ctrl+$ _ Ctrl+Space | UnderBar[x] | |
| x | Style[x,Bold] | x |
option | typical default value | |
| SingleLetterItalics | False | whether to use italics for single‐letter symbol names |
| MultiLetterItalics | False | whether to use italics for multi-letter symbol names |
| SingleLetterStyle | None | the style name or directives to use for single-letter symbol names |
| MultiLetterStyle | None | the style name or directives to use for multi-letter symbol names |
It is conventional in traditional mathematical notation that names consisting of single ordinary English letters are normally shown in italics, while other names are not. If you use TraditionalForm, then the Wolfram Language will by default follow this convention. You can explicitly specify whether you want the convention followed by setting the SingleLetterItalics option for particular cells or cell styles. You can further specify styles for names using single English letters or multiple English letters by specifying values for the options SingleLetterStyle and MultiLetterStyle.
Greek Letters
You can use Greek letters as the names of symbols. The only Greek letter with a built‐in meaning in StandardForm is 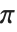 , which the Wolfram Language takes to stand for the symbol Pi.
, which the Wolfram Language takes to stand for the symbol Pi.
Note that even though 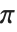 on its own is assigned a built‐in meaning, combinations such as
on its own is assigned a built‐in meaning, combinations such as 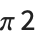 or
or  have no built‐in meanings.
have no built‐in meanings.
The Greek letters 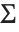 and
and 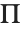 look very much like the operators for sum and product. But as discussed above, these operators are different characters, entered as ∖[Sum] and ∖[Product], respectively.
look very much like the operators for sum and product. But as discussed above, these operators are different characters, entered as ∖[Sum] and ∖[Product], respectively.
Some capital Greek letters such as ∖[CapitalAlpha] look essentially the same as capital English letters. The Wolfram Language, however, treats them as different characters, and in TraditionalForm it uses ∖[CapitalBeta], for example, to denote the built‐in function Beta.
Following common convention, lowercase Greek letters are rendered slightly slanted in the standard fonts provided with the Wolfram System, while capital Greek letters are unslanted. On Greek systems, however, the Wolfram System will render all Greek letters unslanted so that standard Greek fonts can be used.
Almost all Greek letters that do not look similar to English letters are widely used in science and mathematics. The capital xi  is rare, though it is used to denote the cascade hyperon particles, the grand canonical partition function, and regular language complexity. The capital upsilon
is rare, though it is used to denote the cascade hyperon particles, the grand canonical partition function, and regular language complexity. The capital upsilon 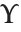 is also rare, though it is used to denote
is also rare, though it is used to denote 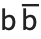 particles, as well as the vernal equinox.
particles, as well as the vernal equinox.
Curly Greek letters are often assumed to have different meanings from their ordinary counterparts. Indeed, in pure mathematics a single formula can sometimes contain both curly and ordinary forms of a particular letter. The curly pi  is rare, except in astronomy.
is rare, except in astronomy.
The final sigma  is used for sigmas that appear at the ends of words in written Greek; it is not commonly used in technical notation.
is used for sigmas that appear at the ends of words in written Greek; it is not commonly used in technical notation.
The digamma 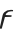 , koppa
, koppa  , stigma
, stigma  , and sampi
, and sampi  are archaic Greek letters. These letters provide a convenient extension to the usual set of Greek letters. They are sometimes needed in making correspondences with English letters. The digamma corresponds to an English w, and koppa to an English q. Digamma is occasionally used to denote the digamma function PolyGamma[x].
are archaic Greek letters. These letters provide a convenient extension to the usual set of Greek letters. They are sometimes needed in making correspondences with English letters. The digamma corresponds to an English w, and koppa to an English q. Digamma is occasionally used to denote the digamma function PolyGamma[x].
Variants of English Letters
By using menu items in the notebook front end, you can make changes in the font and style of ordinary text. However, such changes are usually discarded whenever you send input to the Wolfram Language kernel.
Script, gothic, and double‐struck characters are, however, treated as fundamentally different from their ordinary forms. This means that even though a C that is italic or a different size will be considered equivalent to an ordinary C when fed to the kernel, a double‐struck 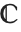 will not.
will not.
Different styles and sizes of C are treated as the same by the kernel. But gothic and double‐struck characters are treated as different:
In standard mathematical notation, capital script and gothic letters are sometimes used interchangeably. The double‐struck letters, sometimes called blackboard or openface letters, are conventionally used to denote specific sets. Thus, for example, 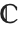 conventionally denotes the set of complex numbers, and
conventionally denotes the set of complex numbers, and 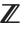 the set of integers.
the set of integers.
Dotless i and j are not usually taken to be different in meaning from ordinary i and j; they are simply used when overscripts are being placed on the ordinary characters.
full names | aliases | |
EscscaEsc – EscsczEsc | lowercase script letters | |
EscscAEsc – EscscZEsc | uppercase script letters | |
EscgoaEsc – EscgozEsc | lowercase gothic letters | |
EscgoAEsc – EscgoZEsc | uppercase gothic letters | |
EscdsaEsc – EscdszEsc | lowercase double‐struck letters | |
EscdsAEsc – EscdsZEsc | uppercase double‐struck letters | |
Esc$aEsc – Esc$zEsc | lowercase formal letters | |
Esc$AEsc – Esc$ZEsc | uppercase formal letters | |
Formal Symbols
Symbols represented by formal letters, or formal symbols, appear in the output of certain functions. They are indicated by gray dots below the English letter.
DifferentialRoot automatically chooses the names for the function arguments:
Formal symbols are Protected, so they cannot be accidentally assigned a value.
Formal symbols can be temporarily modified inside a Block because Block clears all definitions associated with a symbol, including Attributes. Table works essentially like Block, thus also allowing temporary changes.
In most situations modifying formal symbols is not necessary. Since in DifferentialRoot formal symbols are used as names for the formal parameters of a function, the function should simply be evaluated for the actual values of arguments.
The formatting rules were attached to MakeBoxes. Restore the original formatting:
Hebrew Letters
Hebrew characters are used in mathematics in the theory of transfinite sets;  is for example used to denote the total number of integers.
is for example used to denote the total number of integers.
Units and Letter‐like Mathematical Symbols
The Wolfram Language treats  or \[Degree] as the symbol Degree, so that, for example, 30° is equivalent to 30Degree.
or \[Degree] as the symbol Degree, so that, for example, 30° is equivalent to 30Degree.
Note that 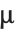 ,
,  , and
, and  are all distinct from the ordinary letters
are all distinct from the ordinary letters 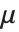 (\[Mu]),
(\[Mu]),  (\[CapitalARing]), and
(\[CapitalARing]), and 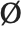 (\[CapitalOSlash]).
(\[CapitalOSlash]).
The Wolfram Language interprets  as Infinity,
as Infinity, 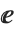 as E, and both
as E, and both  and
and 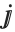 as I. The characters
as I. The characters 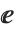 ,
,  , and
, and 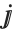 are provided as alternatives to the usual uppercase letters E and I.
are provided as alternatives to the usual uppercase letters E and I.
Shapes, Icons, and Geometrical Constructs
Shapes are most often used as "dingbats" to emphasize pieces of text. But the Wolfram Language treats them as letter‐like forms, and also allows them to appear in the names of symbols.
In addition to shapes such as \[EmptySquare], there are characters such as \[Square], which are treated by the Wolfram Language as operators rather than letter‐like forms.
Since the Wolfram Language treats characters like  as letter‐like forms, constructs like
as letter‐like forms, constructs like 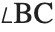 are treated in the Wolfram Language as single symbols.
are treated in the Wolfram Language as single symbols.
Textual Elements
Extended Latin Letters
The Wolfram Language supports all the characters commonly used in Western European languages based on Latin scripts.
Most of the characters shown are formed by adding diacritical marks to ordinary English letters. Exceptions include \[SZ] 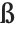 , used in German, and \[Thorn]
, used in German, and \[Thorn] 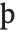 and \[Eth]
and \[Eth]  , used primarily in Old English.
, used primarily in Old English.
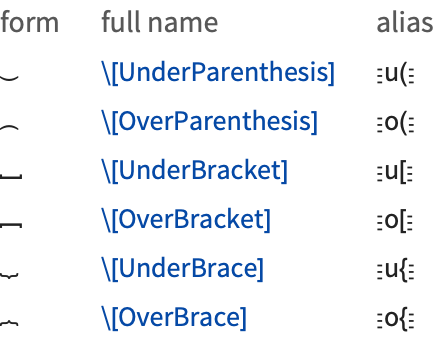
char Ctrl+& mark Ctrl+Space | add a mark above a character |
char Ctrl+$ mark Ctrl+Space | add a mark below a character |
form | alias | full name | |
| ' |
(keyboard character)
| \[RawQuote] | acute accent |
| ′ |
Esc
| \[Prime] | acute accent |
| ` |
(keyboard character)
| \[RawBackquote] | grave accent |
| ‵ |
Esc
`Esc
| \[ReversePrime] | grave accent |
| . . |
(keyboard characters)
| umlaut or diaeresis | |
| ^ |
(keyboard character)
| \[RawWedge] | circumflex or hat |
| ◦ |
Esc
esciEsc
| \[EmptySmallCircle] | ring |
| . |
(keyboard character)
| \[RawDot] | dot |
| ~ |
(keyboard character)
| \[RawTilde] | tilde |
| _ |
(keyboard character)
| \[RawUnderscore] | bar or macron |
| ˇ |
Esc
hckEsc
| \[Hacek] | hacek or check |
| ˘ |
Esc
bvEsc
| \[Breve] | breve |
| |
Esc
dbvEsc
| \[DownBreve] | tie accent |
| ″ |
Esc
| \[DoublePrime] | long umlaut |
| ¸ |
Esc
cdEsc
| \[Cedilla] | cedilla |
Basic Mathematical Operators
| x×y | Times[x,y] | multiplication |
| x÷y | Divide[x,y] | division |
| √x | Sqrt[x] | square root |
| xy | Cross[x,y] | vector cross product |
| ±x | PlusMinus[x] |
(no built
‐
in meaning)
|
| x±y | PlusMinus[x,y] |
(no built
‐
in meaning)
|
| ∓x | MinusPlus[x] |
(no built
‐
in meaning)
|
| x∓y | MinusPlus[x,y] |
(no built
‐
in meaning)
|
Operators in Calculus and Algebra
Logical and Other Connectives
The operators  ,
, 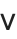 , and
, and  are interpreted as corresponding to the built‐in functions And, Or, and Not, and are equivalent to the keyboard operators &&, ||, and !. The operators
are interpreted as corresponding to the built‐in functions And, Or, and Not, and are equivalent to the keyboard operators &&, ||, and !. The operators 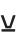 ,
,  , and
, and  correspond to the built‐in functions Xor, Nand, and Nor. Note that
correspond to the built‐in functions Xor, Nand, and Nor. Note that  is a prefix operator.
is a prefix operator.
xy and x⥰y are both taken to give the built‐in function Implies[x,y]. x∈y gives the built‐in function Element[x,y].
The Wolfram Language supports most of the standard syntax used in mathematical logic. In the Wolfram Language, however, the variables that appear in the quantifiers  ,
,  , and
, and  must appear as subscripts. If they appeared directly after the quantifier symbols then there could be a conflict with multiplication operations.
must appear as subscripts. If they appeared directly after the quantifier symbols then there could be a conflict with multiplication operations.
Operators Used to Represent Actions
Following the Wolfram Language's usual convention, all the operators in the table are interpreted to give functions whose names are exactly the names of the characters that appear in the operators.
All the operators in the table above, except for  , are infix, so that they must appear in between their operands.
, are infix, so that they must appear in between their operands.
Bracketing Operators
| ⌊x⌋ | Floor[x] |
| ⌈x⌉ | Ceiling[x] |
| m〚i,j,…〛 | Part[m,i,j,…] |
| 〈x,y,…〉 | AngleBracket[x,y,…] |
| x,y,… | BracketingBar[x,y,…] |
| x,y,… | DoubleBracketingBar[x,y,…] |
Operators Used to Represent Relations
The special character  (or ∖[Equal]) is an alternative input form for ==.
(or ∖[Equal]) is an alternative input form for ==.  is used both for input and output:
is used both for input and output:
Operators Based on Arrows and Vectors
Operators based on arrows are often used in pure mathematics and elsewhere to represent various kinds of transformations or changes.
|
|
\[Null] does not display, but can take modifications such as superscripts:
The \[AlignmentMarker] does not display, but shows how to line up the elements of the column:
The \[ImplicitPlus] operator is used as a hidden plus sign in mixed fractions:
|
|
|
|
In the buttons in a palette, you often want to set up a template with placeholders to indicate where expressions should be inserted. \[SelectionPlaceholder] marks the position where an expression that is currently selected should be inserted when the contents of the button are pasted. \[Placeholder] marks other positions where subsequent expressions can be inserted. The Tab key will take you from one such position to the next.
|
|
In describing how to enter input into the Wolfram System, it is sometimes useful to give explicit representations for keys you should press. You can do this using characters like ↵ and . Note that ␣ and are actually treated as spacing characters by the Wolfram Language.
|
|
The Wolfram Language uses a \[Continuation] character to indicate that the number continues onto the next line:
The fonts that are distributed with the Wolfram System contain their own renderings of many ordinary keyboard characters. The reason for this is that standard system fonts often do not contain appropriate renderings. For example, ^ and ~ are often drawn small and above the centerline, while for clarity in the Wolfram Language they must be drawn larger and centered on the centerline.