ArcSinDistribution
ArcSinDistribution[{xmin,xmax}]
represents the arc sine distribution supported between xmin and xmax.
represents the arc sine distribution supported between zero and one.
Details
- The probability density for value
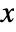in an arc sine distribution is proportional to 
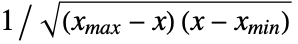for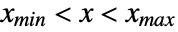 
, and is zero f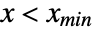or 
or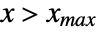 
. - ArcSinDistribution allows xmin and xmax to be any real numbers with xmin<xmax.
- ArcSinDistribution allows xmin and xmax to be any quantities of the same unit dimensions. »
- ArcSinDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- ArcSinDistribution[{xmin,xmax}] represents a particular statistical distribution defined for values between xmin and xmax. It is named for the functional form of its cumulative distribution function (CDF), which is a normalized arc sine function. Its probability density function (PDF) is concave up, attains its absolute minimum at and has reflective symmetry about the midpoint of its domain, and has potential singularities (where it asymptotically approaches infinity) at points near both xmin and xmax.
- The arc sine distribution arises naturally in a number of mathematical contexts, including probability theory and number theory. Much of the overall behavior of a one-dimensional Wiener process is described by three so-called arc sine laws attributed to Lévy. These laws state that the proportion of time for which the process is positive, the time of its last zero, and the times at which it achieves a maximum are all arc sine-distributed. A number theoretic result attributed to Erdős relates the arc sine distribution to the number of small prime divisors of a given integer. More recently, the arc sine distribution has also been shown to be the limiting distribution for probabilistic models of quantum coin flips.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from an arc sine distribution. Distributed[x,ArcSinDistribution[{xminxmax}]], written more concisely as xArcSinDistribution[{xminxmax}], can be used to assert that a random variable x is distributed according to an arc sine distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be returned using PDF[ArcSinDistribution[{xmin,xmax}],x] and CDF[ArcSinDistribution[{xmin,xmax}],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with an arc sine distribution, EstimatedDistribution to estimate an arc sine parametric distribution from given data, and FindDistributionParameters to fit data to an arc sine distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic arc sine distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic arc sine distribution.
- TransformedDistribution can be used to represent a transformed arc sine distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain an arc sine distribution and ProductDistribution can be used to compute a joint distribution with independent component distributions involving arc sine distributions.
- The arc sine distribution is closely related to a number of other distributions. For example, the standard arc sine distribution ArcSinDistribution[{0,1}] is precisely equal to the beta distribution BetaDistribution[1/2,1/2]. As a result, ArcSinDistribution inherits many of the relationships of the BetaDistribution. ArcSinDistribution can likewise be viewed as a type-1 PearsonDistribution in the sense that PDF[ArcSinDistribution[{0,1}],x] is equal to PDF[PearsonDistribution[1,1,-1/2,1,-1,0],x]. It is also closely related to UniformDistribution, PERTDistribution, ChiSquareDistribution, GammaDistribution, and BetaPrimeDistribution.
Examples
open allclose allBasic Examples (4)
Scope (7)
Generate a sample of pseudorandom numbers from an arc sine distribution:
Compare the histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
Skewness and kurtosis are constant:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (5)
Simulate the proportion of the time spent on the positive side by a symmetric random walk:
Calculate the ratio of time spent on the positive side:
In the limit, the ratio has ArcSinDistribution:
Simulate the proportion of time spent on the positive side by a standard WienerProcess:
In the limit, the ratio follows ArcSinDistribution:
Find the distribution of the last time WienerProcess changed sign between times 0 and 1:
Calculate the differences of signs to find sign changes:
Extract paths and find times of the last sign change for each path:
In the limit, the times follow ArcSinDistribution:
Find the distribution of the time corresponding to the maximum value of WienerProcess between 0 and 1:
From each path, extract the times corresponding to the maximum for that path:
In the limit, the times follow ArcSinDistribution:
Discrete-time Markov chain 
, where 
is the sequence of independent and identically distributed (iid) standard uniform random variables, and 
is the sequence of iid symmetric Bernoulli random variables converges to stationary distribution ArcSinDistribution[{0,1}] for any initial condition 
such that 
:
Sample a realization of the Markov chain and discard the burn-in portion of the path:
Samples from the Markov chain are not independent and exhibit internal structure:
Compare the histogram of path values to the PDF of the Markov chain's stationary distribution:
Properties & Relations (9)
Arc sine distribution is closed under translation and scaling by a positive factor:
The CDF of arc sine distribution is proportional to the ArcSin function:
The square of an arc sine distribution over 
has arc sine distribution over 
:
Relationships to other distributions:
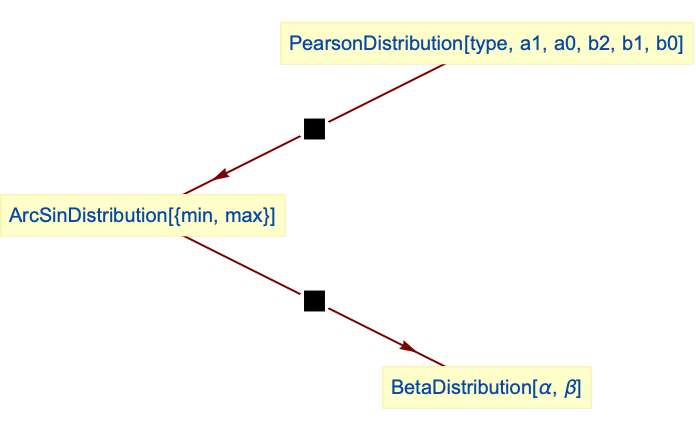
BetaDistribution is a special case of arc sine distribution:
Arc sine distribution is a special type of type 1 PearsonDistribution:
ArcSinDistribution is a transformation of UniformDistribution:
ArcSinDistribution is a transformation of TriangularDistribution:
HoytDistribution can be obtained from ExponentialDistribution and ArcSinDistribution:
Text
Wolfram Research (2010), ArcSinDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/ArcSinDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "ArcSinDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ArcSinDistribution.html.
APA
Wolfram Language. (2010). ArcSinDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ArcSinDistribution.html