BenktanderWeibullDistribution[a,b]
represents a Benktander distribution of type II with parameters a and b.


BenktanderWeibullDistribution
BenktanderWeibullDistribution[a,b]
represents a Benktander distribution of type II with parameters a and b.
Details
- The probability density for a value
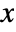 in a Benktander–Weibull distribution is proportional to
in a Benktander–Weibull distribution is proportional to 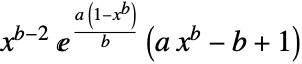 for
for 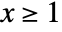 .
. - BenktanderWeibullDistribution allows a to be any positive real number and
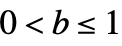 .
. - BenktanderWeibullDistribution allows a and b to be dimensionless quantities. »
- BenktanderWeibullDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- BenktanderWeibullDistribution[a,b] represents a continuous statistical distribution defined over the interval
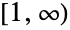 and parametrized by positive values a and b,
and parametrized by positive values a and b, 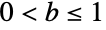 . The parameters a and b determine the overall shape of the probability density function (PDF) of a Benktander–Weibull distribution, though the PDF is monotonic decreasing with potential singularities approaching the leftmost boundary of its domain for all such parameters. The tails of the PDF of BenktanderWeibullDistribution are "heavy" (in the sense that the PDF decreases more slowly than exponentially for large values of
. The parameters a and b determine the overall shape of the probability density function (PDF) of a Benktander–Weibull distribution, though the PDF is monotonic decreasing with potential singularities approaching the leftmost boundary of its domain for all such parameters. The tails of the PDF of BenktanderWeibullDistribution are "heavy" (in the sense that the PDF decreases more slowly than exponentially for large values of 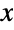 ), though the distribution is considered "subexponential" rather than "fat-tailed". (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.)
), though the distribution is considered "subexponential" rather than "fat-tailed". (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) - Benktander–Weibull distributions were formulated by Swedish actuary Gunnar Benktander, who noted that empirical mean excess functions suggest the need for distributions that are "intermediate" between the Pareto and exponential distributions. Most commonly, Benktander–Weibull distributions are used to model asset loss within actuarial science applications. Moreover, subexponential distributions such as the Benktander–Weibull are also useful in studying the properties of random walks. Benktander–Weibull distributions are sometimes called type II Benktander distributions, with the first type often known as the Benktander–Gibrat distribution and implemented as BenktanderGibratDistribution in the Wolfram Language. Both are considered to be "close to" Weibull distributions, in the sense that the PDFs of the two distributions are qualitatively similar.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Benktander–Weibull distribution. Distributed[x,BenktanderWeibullDistribution[a,b]], written more concisely as xBenktanderWeibullDistribution[a,b], can be used to assert that a random variable x is distributed according to a Benktander–Weibull distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[BenktanderWeibullDistribution[a,b],x] and CDF[BenktanderWeibullDistribution[a,b],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a Benktander–Weibull distribution, EstimatedDistribution to estimate a Benktander–Weibull parametric distribution from given data, and FindDistributionParameters to fit data to a Benktander–Weibull distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Benktander–Weibull distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Benktander–Weibull distribution.
- TransformedDistribution can be used to represent a transformed Benktander–Weibull distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Benktander–Weibull distribution and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Benktander–Weibull distributions.
- BenktanderWeibullDistribution is related to a number of other statistical distributions. For example, as previously noted, both BenktanderWeibullDistribution and BenktanderGibratDistribution belong to the same "family" of distributions, namely those that are considered intermediate between ParetoDistribution and ExponentialDistribution. Qualitatively, the PDF of BenktanderWeibullDistribution is similar to that of WeibullDistribution, thus inducing (qualitative) relationships between BenktanderWeibullDistribution and a number of distributions, including GammaDistribution, RayleighDistribution, MaxStableDistribution, MinStableDistribution, ExtremeValueDistribution, GumbelDistribution, and FrechetDistribution. BenktanderWeibullDistribution[a,1] is a truncated version of ExponentialDistribution[a], in the sense that the PDF of the former with respect to x is precisely equal to PDF[TruncatedDistribution[{1,Infinity},ExponentialDistribution[a]],x]. Likewise, BenktanderWeibullDistribution can be viewed as a shifted ExponentialDistribution. ParetoDistribution is considered a limiting case of BenktanderWeibullDistribution, in the sense that the PDF of BenktanderWeibullDistribution[a,b] tends to that of ParetoDistribution[1,a+1] whenever b tends to 0. This fact implies that the PDFs of both BenktanderWeibullDistribution[a,b] and BenktanderGibratDistribution[a,b] approach the same limiting function as b tends to 0. Furthermore, the survival function of a stationary renewal distribution associated with a Benktander–Weibull distribution has precisely the same formula on its domain as the survival function of the truncated Weibull distribution TruncatedDistribution[{1,∞},WeibullDistribution[b,(b/a)1/b]].
Examples
open all close allBasic Examples (4)
Scope (8)
Generate a sample of pseudorandom numbers from a Benktander–Weibull distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Use dimensionless Quantity to define BenktanderWeibullDistribution:
Applications (2)
Compute the mean excess function for a Benktander type II distribution:
For large ![]() , it approaches that of a Weibull distribution:
, it approaches that of a Weibull distribution:
Now replace the incomplete ![]() function with its asymptotics at large arguments:
function with its asymptotics at large arguments:
Find a stationary renewal distribution associated with a Benktander type II distribution:
Compare with a truncated WeibullDistribution:
Properties & Relations (5)
BenktanderWeibullDistribution is subexponential for ![]() :
:
Relationships to other distributions:
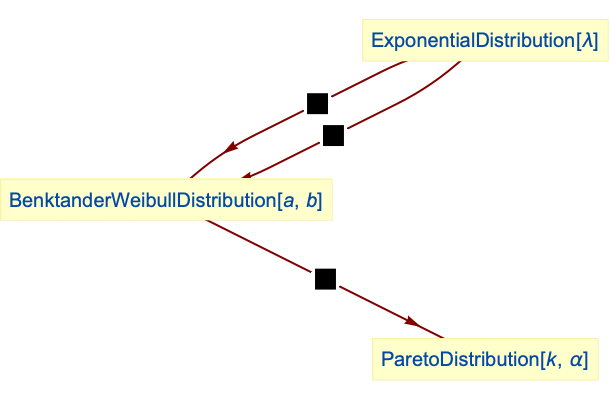
When ![]() , Benktander type II reduces to a truncated ExponentialDistribution:
, Benktander type II reduces to a truncated ExponentialDistribution:
Shifted ExponentialDistribution is a Benktander type II distribution:
A ParetoDistribution is the limiting case of the Benktander type II distribution:
Related Guides
Text
Wolfram Research (2010), BenktanderWeibullDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/BenktanderWeibullDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "BenktanderWeibullDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/BenktanderWeibullDistribution.html.
APA
Wolfram Language. (2010). BenktanderWeibullDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BenktanderWeibullDistribution.html
BibTeX
@misc{reference.wolfram_2025_benktanderweibulldistribution, author="Wolfram Research", title="{BenktanderWeibullDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/BenktanderWeibullDistribution.html}", note=[Accessed: 24-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_benktanderweibulldistribution, organization={Wolfram Research}, title={BenktanderWeibullDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/BenktanderWeibullDistribution.html}, note=[Accessed: 24-February-2026]}