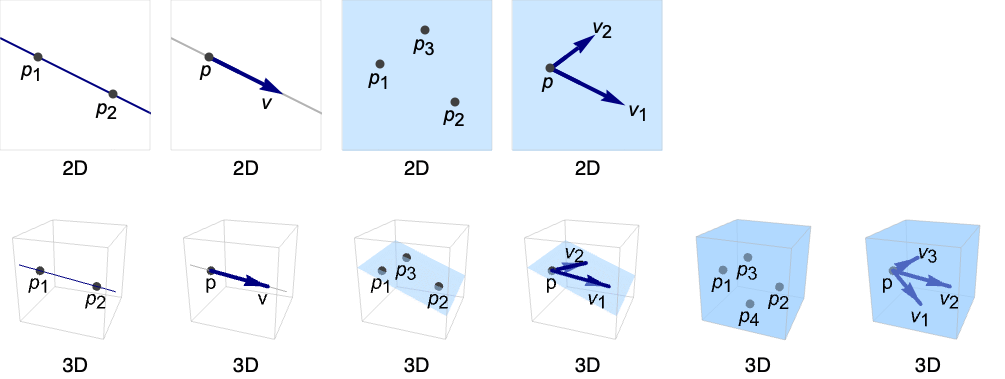
AffineSpace

AffineSpace[{p1,…,pk+1}]

点 piを通るアフィン空間を表す．

AffineSpace[p,{v1,…,vk}]

vi方向に p を通るアフィン空間を表す．

詳細

  • AffineSpaceは，点，線，平面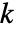，-フラット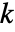，-平面等としても知られている．
  • AffineSpaceは，幾何学領域およびグラフィックスプリミティブとして使うことができる．
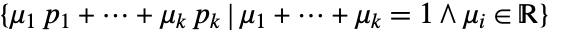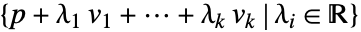  • AffineSpaceは，領域あるいはを表す．piがアフィン独立あるいは viが線形独立の場合，次元は k である．
  • AffineSpaceはGraphicsおよびGraphics3Dで使うことができる．
  • AffineSpaceは，描画の際はPlotRangeで切り取られる．
  • グラフィックス描画は，Opacity等の指示子および色の影響を受ける．
  • PointSize零次元()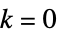
    Thickness,Dashing一次元()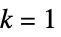
    FaceForm二次元()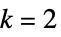
  • 二次元のAffineSpaceについては，FaceForm[front,back]を使って front と back に別々のスタイルを指定することができる．ただし，front は，どちらの入力形式が使われているかによって，通常のCross[v1,v2]あるいはCross[p2-p1,p3-p1]の向きであると定義される．

例題

すべて開くすべて閉じる

例  (3)

2DのAffineSpace：

3Dのもの：

アフィン空間領域にさまざまなスタイルを適用する：

点が指定されたアフィン空間領域に含まれるかどうかを調べる：

スコープ  (17)

グラフィックス  (7)

指定  (2)

点を使って3Dアフィン空間を定義する：

1つの点と2つの接ベクトルを使って同じアフィン空間を定義する：

1つの点と1つの接ベクトルで定義された3Dアフィン空間：

方向が異なるアフィン空間：

スタイル付け  (2)

色指示子でアフィン空間の色を指定する：

FaceFormおよびEdgeFormを使って面と辺のスタイルを指定する：

座標  (3)

プロット範囲との割合で座標を指定する：

通常の座標からスケールされたオフセットを指定する：

点とベクトルはDynamicでよい：

領域  (10)

埋込み次元は座標の次元である：

幾何次元は領域それ自体の次元である：

点の帰属判定：

帰属条件を得る：

アフィン空間は無限測度と未定義の重心を持つ：

点からの距離：

点からの符号付き距離：

領域内の最近点：

最近点：

アフィン空間は非有界である：

領域範囲を求める：

アフィン空間上で積分する：

アフィン空間上で最適化する：

アフィン空間上で方程式を解く：

アプリケーション  (24)

座標系  (4)

座標軸を可視化する：

3Dで：

座標平面を可視化する：

プロットにドロップラインを加える：

プロットにドロップ平面を加える：

変換の可視化  (3)

RotationTransformについての回転軸を可視化する：

3Dの回転された座標軸を可視化する：

反射面を可視化する：

反射面を定義する：

平面上の点とその法線ベクトルを使ってReflectionTransformを定義する：

平面についての単位立方体の反射を可視化する：

プロットの図解  (3)

漸近線を示す：

Histogram上のMeanを示す：

BubbleChart中の分割空間：

グラフィックスを組み合せる：

交点を求める  (10)

2本の線の交点を求める：

これをプロットする：

線と円の交点を求める：

これをプロットする：

5本のランダムな線のペアごとの全交点を求める：

BooleanCountingFunctionを使って厳密に2つの条件が真であることを表す：

これをプロットする：

線と平面の交点を求める：

これをプロットする：

線と平面の交点を求める：

これをプロットする：

線と四面体の境界の交点を求める：

これをプロットする：

三角形の高さを求める：

高さを赤で可視化する：

三角形が埋め込まれている平面を求める：

InfinitePlaneはTriangleと同じパラメータ化を使うことができる：

多角形が埋め込まれている平面を求める：

平面を求めるためには，最初の3点（あるいは直線上にない任意の3点）を取る：

球，平面，で定義される曲面の交点を求める：

交点を可視化する：

線，平面，空間の構成  (4)

平行線は平行な方向ベクトルを持つ：

平行ベクトルの角度はあるいは である：

3Dにおける平行平面は平行な法線ベクトルを持つ：

法線は平行である：

垂直線は直交の接ベクトルと直交の法線ベクトルを持つ：

接ベクトルは直交する：

法線もまた直交する：

垂直平面は直交する法線ベクトルを持つ：

法線ベクトルは直交する：

すべてのベクトル が によって生成された線形空間にあるか，あるいはすべてのベクトル が によって生成された線形空間にある場合，AffineSpace[p,vv1]はAffineSpace[q,vv2]と平行である：

2つのアフィン空間が平行かどうかを調べるために，と の和集合の階数が と の階数の最大のものと等しいかどうかをチェックする：

平面と4D空間の3Dアフィン部分空間が平行かどうかを調べる：

特性と関係  (6)

AffineSpaceはConicHullRegionの特殊ケースである：

InfiniteLineはAffineSpaceの特殊ケースである：

InfinitePlaneはAffineSpaceの特殊ケースである：

HyperplaneはAffineSpaceの特殊ケースである：

ParametricRegionは，における任意のAffineSpaceを表すことができる：

:における：

ImplicitRegionは内の任意のAffineSpaceを表すことができる：

内：

おもしろい例題  (4)

線のランダムな集合：

線の組織化された集合：

平面のランダムな集合：

無限平面を軸の周りで回転させる：

Wolfram Research (2015), AffineSpace, Wolfram言語関数， https://reference.wolfram.com/language/ref/AffineSpace.html.

テキスト

Wolfram Research (2015), AffineSpace, Wolfram言語関数， https://reference.wolfram.com/language/ref/AffineSpace.html.

CMS

Wolfram Language. 2015. "AffineSpace." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AffineSpace.html.

APA

Wolfram Language. (2015). AffineSpace. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AffineSpace.html

BibTeX

@misc{reference.wolfram_2024_affinespace, author="Wolfram Research", title="{AffineSpace}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/AffineSpace.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_affinespace, organization={Wolfram Research}, title={AffineSpace}, year={2015}, url={https://reference.wolfram.com/language/ref/AffineSpace.html}, note=[Accessed: 21-November-2024 ]}