AffineSpace
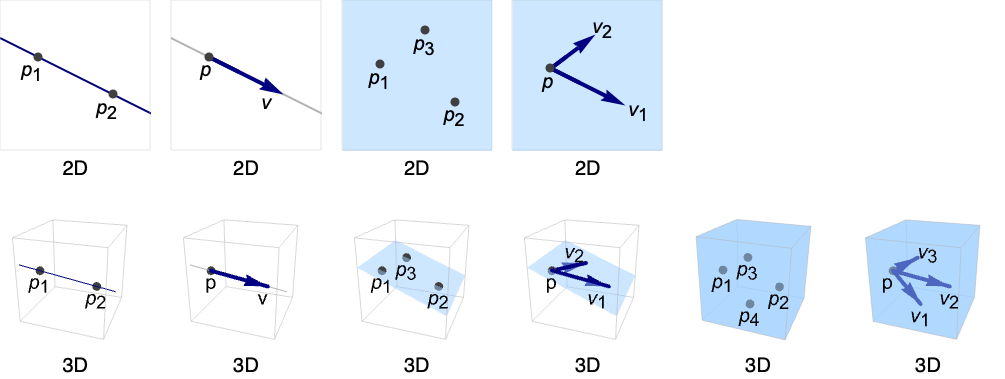
AffineSpace[{p1,…,pk+1}]
表示通过点 pi 的仿射空间.
AffineSpace[p,{v1,…,vk}]
表示在方向 vi 上通过点 p 的仿射空间.
更多信息

- AffineSpace 也被称作点、直线、平面、
 -flat、
-flat、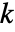 -平面等.
-平面等. - AffineSpace 可以用作几何区域和图形基元.
- AffineSpace 表示区域
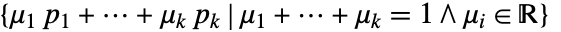 或
或 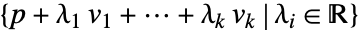 . 如果 pi 仿射独立或者 vi 线性独立,则维数为 k.
. 如果 pi 仿射独立或者 vi 线性独立,则维数为 k. - AffineSpace 可用于 Graphics 和 Graphics3D.
- 当渲染时,AffineSpace 将被 PlotRange 剪切.
- 图形渲染受诸如 Opacity 等指令和颜色以及下面的影响:
-
PointSize 0维 ( 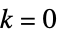 )
)Thickness,Dashing 1维 ( 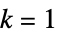 )
)FaceForm 2维 ( 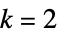 )
) - 对于二维 AffineSpace,FaceForm[front,back] 可用于指定 front 和 back 的不同样式,其中 front 根据所用的输入形式,在正态 Cross[v1,v2] 或 Cross[p2-p1,p3-p1] 方向上被定义.
范例
打开所有单元关闭所有单元基本范例 (3)
范围 (17)
图形 (7)
应用 (24)
可视化变换 (3)
可视化 RotationTransform 的轴旋转:
使用平面上的点及其法向量定义 ReflectionTransform:
插图 (3)
求交点 (10)
使用 BooleanCountingFunction 表示恰好有两个条件为真:
AffineSpace 可使用与 Triangle 相同的参数:
线、平面和空间的排列 (4)
如果所有的向量 ![]() 属于由
属于由 ![]() 生成的线性空间,或者所有向量
生成的线性空间,或者所有向量 ![]() 属于由
属于由 ![]() 生成的线性空间,则AffineSpace[p,vv1] 与 AffineSpace[q,vv2] 平行:
生成的线性空间,则AffineSpace[p,vv1] 与 AffineSpace[q,vv2] 平行:
属性和关系 (6)
AffineSpace 是 ConicHullRegion 的特例:
InfiniteLine 是 AffineSpace 的特例:
InfinitePlane 是 AffineSpace 的特例:
Hyperplane 是 AffineSpace 的特例:
ParametricRegion 可以表示 ![]() 中的任意 AffineSpace:
中的任意 AffineSpace:
ImplicitRegion 可以表示 ![]() 中的任意 AffineSpace:
中的任意 AffineSpace:
文本
Wolfram Research (2015),AffineSpace,Wolfram 语言函数,https://reference.wolfram.com/language/ref/AffineSpace.html.
CMS
Wolfram 语言. 2015. "AffineSpace." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/AffineSpace.html.
APA
Wolfram 语言. (2015). AffineSpace. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/AffineSpace.html 年