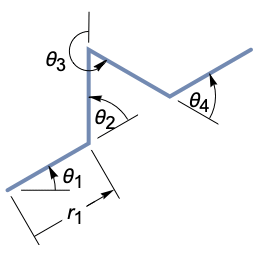
AnglePath

AnglePath[{θ1,θ2,θ3,…}]

给出由二维坐标组成的列表，对应的是从 {0,0} 开始的一条路径，后续的每一步都是单位长度且和前一步的相对夹角为 θi.

AnglePath[{{r1,θ1},{r2,θ2},{r3,θ3},…}]

返回路径的相续步长为 ri.

AnglePath[θ0,{step1,step2,…}]

相对于 轴的起始角度为 θ0.

AnglePath[{x,y},{step1,step2,…}]

从点 {x,y} 开始，相对于 轴的起始角度为 0.

AnglePath[{{x,y},θ0},{step1,step2,…}]

从点 {x,y} 开始，相对于 轴的起始角度为 θ0.

AnglePath[{{x,y},{dx,dy}},{step1,step2,…}]

第一步是从点 {x,y} 到 {x+dx,y+dy}.

AnglePath[init,steps,form]

每步返回由 form 指定的形式的数据.

更多信息和选项

  • 对生成路径时到达的每一个点，AnglePath 实际上先旋转指定的相对角度，再前进指定的距离.
  • 除非显式的以 Quantity 对象的形式给出，角度 θi 假设是以弧度为单位，正方向为逆时针方向.（乘以 Degree 就可以转换为角度单位.）
  • 在 AnglePath[{θ1,θ2,θ3,…}] 中角度 θ1 假设是相对于 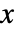轴的.
  • AnglePath[…,form] 中 form 的可能选择包括：
  • "Position"笛卡尔坐标 {xi,yi} (默认)
    "FrameMatrix"相对于初始标架的当前标架的旋转矩阵
    "RelativeMatrix"相对于之前标架的当前标架的旋转矩阵
    "FrameAngle"相对于初始步长的旋转角度
    "RelativeAngle"相对于之前步长的旋转角度
    "Translation"根据初始步长的平移变换
    "Rotation"根据初始步长的旋转变换
    "RotationTranslation"根据初始步长的旋转平移变换
    {form1,form2,…}格式列表
  • AnglePath 的参数可以是符号. 它们也可以是 Quantity 对象.
  • AnglePath 有一个 WorkingPrecision 选项，确定了生成数字的精度.
  • 采用默认设置 WorkingPrecisionAutomatic 的情况下，只为相当短的路径的精确输入生成精确数字；对于较长的路径，将使用机器精度.

范例

打开所有单元关闭所有单元

基本范例  (5)

从 {0,0} 开始沿着 轴，前进若干单位步长，每步旋转 90°：

三段的折线：

前进 20 步，每步总是左转 110°：

产生路径的转换函数：

把它们应用于乌龟：

使用符号输入：

范围  (13)

步长规范  (3)

按指定的一系列角度前进单位步长，从 轴开始：

指定每一步的长度：

在输入中使用 Quantity 对象：

路径初始化  (4)

指定初始位置：

指定初始方向：

指定初始位置和方向：

使用笛卡尔坐标 {dx,dy} 指定初始方向：

输出格式  (6)

默认情况下，AnglePath 返回每一步的位置：

计算每个局部标架相对于之前局部标架的方向：

计算每个局部标架相对于整体标架的方向：

计算决定每个局部标架在整体标架方向的角度：

根据初始步长，产生旋转平移变换：

应用于一个三角形：

调用一个 AnglePath ，产生不同的输出类型：

三元组的首个元素是相对于之前标架的旋转矩阵：

第二个元素是位置：

第三个元素根据初始标架的转换函数：

选项  (1)

WorkingPrecision  (1)

默认情况下，AnglePath 为较短路径的精确输入生成精确数字，对于较长的路径，则给出机器数字：

指定无穷大的精度将进行精确但较慢的计算：

在计算中使用指定的精度：

应用  (3)

生成相邻步之间角度改变最多不超过 20° 的随机游走：

生成龙形曲线：

生成科赫雪花曲线：

基于 Thue–Morse 序列的另一种模式：

属性和关系  (5)

角度在后续每一步中被累积，从 θ0 开始：

这两个结果是完全相同的：

取 100 个介于 和 之间的角度：

作为绝对角度考虑的话，它们平均表示一组向右的步进：

作为相对角度考虑的话，路径可能沿任何方向演变. 路径总长度不变：

整体标架旋转可以作为所有之前相关旋转乘积获取：

计算带有以下输入的路径的位置：

每个新的位置可以按沿着初始 x 轴旋转位移进行计算：

可能存在的问题  (1)

当使用 {{x,y},{dx,dy}} 作为第一个参数时，{dx,dy} 确定的是初始的方向，而不是下一个点的位置：

互动范例  (1)

按给定的长度和相对方向移动海龟：

巧妙范例  (4)

绘制线段，每条线段与前一条段形成的角度均匀增加：

绘制线段，相邻的相对角度增加 1 弧度：

绘制线段，相邻的相对角度持续增加，并被 Sin 函数调制：

为角度路径的线段着色：

Wolfram Research (2015)，AnglePath，Wolfram 语言函数，https://reference.wolfram.com/language/ref/AnglePath.html （更新于 2019 年）.

文本

Wolfram Research (2015)，AnglePath，Wolfram 语言函数，https://reference.wolfram.com/language/ref/AnglePath.html （更新于 2019 年）.

CMS

Wolfram 语言. 2015. "AnglePath." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2019. https://reference.wolfram.com/language/ref/AnglePath.html.

APA

Wolfram 语言. (2015). AnglePath. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/AnglePath.html 年

BibTeX

@misc{reference.wolfram_2024_anglepath, author="Wolfram Research", title="{AnglePath}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/AnglePath.html}", note=[Accessed: 05-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_anglepath, organization={Wolfram Research}, title={AnglePath}, year={2019}, url={https://reference.wolfram.com/language/ref/AnglePath.html}, note=[Accessed: 05-November-2024 ]}