Around

Around[x,δ]

x の近くの値で不確かさが δ の，近似された数または量を表す．

Around[x,{δ-,δ+}]

x の近くの値で非対称の不確かさが δ-, δ+の，数または量を表す．

Around[dist]

分布 dist の平均の近くで，不確かさが分布の標準偏差に対応する，近似された数または量を表す．

Around[list]

list の要素の平均近くの近似オブジェクトを，その標準偏差に相当する不確かさとともに与える．

Around[s]

数，区間または文字列指定 s から導かれた近似オブジェクトを与える．

詳細

  • Around[x,δ]は，一般に x±δ として表示される．Around[1.2345678,0.0000012]におけるように x に比べて δ が非常に小さい場合は，代りにのような形式で表示される．
  • Around[x,δ]を使って統計的あるいはその他の不確かさを持つ計測結果を表すことができる．
  • Around[x,Scaled[ϕ]]は，Around[x,ϕ x]に相当する，相対誤差 ϕ の数を表す．
  • Aroundが計算に使われる場合，デフォルトで，不確かさは相関しないものと仮定して一次級数近似を使って伝播される．
  • Around[…]["prop"]を使って次の特性が抽出できる．
  • "Value"Around[x,δ]の中央値 x
    "Uncertainty"Around[x,δ]の不確かさ δ
    "Number"値 x と δに対応する確度を持つ数
    "Interval"Interval[{x-δ,x+δ}]
  • Around[s]の不確かさを含む数は以下のように指定できる．
  • x（近似数）Around[x,(10^-Accuracy[x])/2]
    Interval[{xmin,xmax}]Around[(xmax+xmin)/2,(xmax-xmin)/2]
    dist（統計分布）Around[Mean[dist],StandardDeviation[dist]]
    list（要素のリスト）Around[Mean[list],StandardDeviation[list]]
    "nn.dddd"（数列）（不確かさは有効桁数で決定される）
  • 線形演算の場合，Around[x,δ]は，値が正規分布NormalDistribution[x,δ]に従って分布している数のように振る舞う．
  • Less，Equal，Greater等の関係演算子をAroundオブジェクトのAround[x1,δ1]とAround[x2,δ2]に使うと，中心 x1と x2が2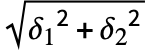より大きいか小さいかによってTrueまたはFalseが返される．数値の場合はAroundオブジェクトと比較する際に不確かさ0が割り当てられる．
  • NumericalOrder[Around[x1,δ1],Around[x2,δ2]]は，中心 x1と x2の間の距離が0.5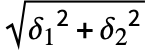より小さければ0を返す．その他の場合は，中心の順序によって1または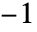を返す．Aroundオブジェクトと数値を数値順にソートする際は，数値に不確かさ0が割り当てられる．
  • Around[x,δ]の値 x と不確かさ δ は任意の数式または記号式でよい．δ が数式なら，x と δ は両方とも数値となる．デフォルトで，機械精度が使われるが，数を忠実に表すために必要であれば，より高い精度を使うこともできる．
  • Around[x,δ]は1桁または2桁の不確かさ δ で表示される．x は小数点の右側に δ と同じ桁数で表示される．
  • Around[x,δ]の x と δ の単位は，互換であれば異なっていてもよい．
  • Around[{x1,x2,…},δ] は第1引数のリストに縫い込まれ，事実上，xiの不確かさは相関しないものとして扱われる．

例題

すべて開くすべて閉じる

例  (10)

さまざまなサイズと不確かさの不確かな数：

さまざまな単位の不確かなQuantityオブジェクト：

非対称の不確かさを持つAroundオブジェクト：

入力で5%の相対的不確かさを指定する：

Aroundオブジェクトを操作する：

Aroundオブジェクトのリストをプロットする：

Aroundオブジェクトの一部を抽出する：

同じAroundオブジェクトの異なる2つの例は相関しないと仮定される：

したがって，結果の不確かさは2倍して得られたものよりも小さい：

記号的なAroundオブジェクトを使う：

それに対して操作を行う：

不確かさが相関しないと仮定される，記号的なAroundオブジェクトを加える：

スコープ  (20)

不確かなオブジェクト  (6)

不確かな数：

非対称な不確かさを持った不確かな数：

不確かなQuantityオブジェクト：

互換単位の値と不確かさを使う：

値と不確かさに同じ単位を使う：

結果は，Aroundの大きさを持つ単一のQuantityオブジェクトである：

互換単位の非対称の不確かさを使う：

同じ不確かさのさまざまな大きさの値：

同じ値に対するさまざまな大きさの不確かさ：

相対的不確かさが30%の不確かな数：

同じオブジェクトをQuantity百分率を使って表す：

任意次元のQuantityの値を使う：

アクセサと変換  (4)

Aroundオブジェクトの値と不確かさを抽出する：

Aroundオブジェクトから有限精度数を作る：

その確度は a の不確かさと一致する：

有限精度数からもとのAroundオブジェクトを再構築する：

Aroundオブジェクトの値を中心とした区間を，その不確かさで与えられた半幅で構築する：

区間からもとのAroundオブジェクトを構築する：

Aroundを使って数を含む文字列を，有効な最終桁の不確かさを0.5と仮定して変換する：

不確かなオブジェクトを使った演算  (4)

数の基本演算：

Quantityオブジェクトの基本演算：

要素がAroundオブジェクトであるQuantityArrayオブジェクトを構築する：

QuantityArray構造を保持したまま操作する：

結果を正規化する：

記号的なAroundオブジェクトの基本演算：

不確かなオブジェクトの比較と順序づけ  (6)

中心が離れた2つのAroundオブジェクトを比較する：

両者の距離は0よりはるかに大きい：

中心が近い2つのAroundオブジェクトを比較する：

両者の距離は0よりはるかに大きくはない：

数のAroundオブジェクトを比較する：

距離は0よりはるかに大きい：

Quantityの中心と不確かさを持つAroundオブジェクトを比較する：

両者の距離は0よりはるかに大きい：

Aroundオブジェクトと数の集まりを数値順に並べる：

速度の集まりを数値順に並べる：

値を直接比較するために共通の基本単位に変換する：

アプリケーション  (3)

不確かさがあるデータをプロットする：

太陽系外惑星の半径と質量を，両方の変数にある不確かさも入れてプロットする：

質量と半径の平均値を計算する：

地球の質量および半径と比較する：

長さの振り子の振動周期を，地球の引力をとし，これらの数量の最終有効桁に1単位の不確かさを仮定して計算する：

特性と関係  (3)

1階級数近似を使ってAroundオブジェクトを二乗する：

TransformedDistributionを使って対応する厳密計算を行う：

高次級数展開を使うと厳密な結果に対するよりよい近似が得られる：

非対称分布に直接Aroundを使うと，非対称な不確かさがあるオブジェクトが返される：

正規分布を取ってこれのシミュレーションを行う：

Around[scalars]は分布の平均と標準偏差を推定する：

Around[dist]は分布 dist における真のパラメータを与える：

MeanAround[scalars]は分布の平均と平均の標準誤差を記述する：

Around[x,δ]とCenteredInterval[x,δ]は数値演算で異なる伝播規則を使う：

Wolfram Research (2019), Around, Wolfram言語関数， https://reference.wolfram.com/language/ref/Around.html （2023年に更新）.

テキスト

Wolfram Research (2019), Around, Wolfram言語関数， https://reference.wolfram.com/language/ref/Around.html （2023年に更新）.

CMS

Wolfram Language. 2019. "Around." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/Around.html.

APA

Wolfram Language. (2019). Around. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Around.html

BibTeX

@misc{reference.wolfram_2024_around, author="Wolfram Research", title="{Around}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/Around.html}", note=[Accessed: 05-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_around, organization={Wolfram Research}, title={Around}, year={2023}, url={https://reference.wolfram.com/language/ref/Around.html}, note=[Accessed: 05-November-2024 ]}