Around

Around[x,δ]

表示一个近似数或量，其值大约为 x，不确定度为 δ.

Around[x,{δ-,δ+}]

表示一个数或量，其值大约为 x，非对称不确定度为 δ-、δ+.

Around[dist]

给出分布 dist 的平均值附近的近似数或量，其不确定度对应于分布的标准差.

Around[list]

给出 list 元素均值附近的近似对象，其不确定度对应于其标准差.

Around[s]

给出根据数字、区间或字符串指定 s 导出的近似对象.

更多信息

  • Around[x,δ] 通常显示为 x±δ. 如果与 x 相比 δ 非常小，如 Around[1.2345678,0.0000012]，则代之以像 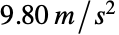这样的形式.
  • Around[x,δ] 可用于表示存在统计或其他不确定性的测量结果.
  • Around[x,Scaled[ϕ]] 表示相对误差为 ϕ 的数字，对应于 Around[x,ϕ x].
  • 当在计算中使用 Around 时，假设没有相关性，默认情况下用一阶级数近似来传播不确定性.
  • 可用 Around[…]["prop"] 提取下列属性：
  • "Value"Around[x,δ] 的中心值 x
    "Uncertainty"Around[x,δ] 中的不确定度 δ
    "Number"值为 x，准确度为 δ 的数字
    "Interval"Interval[{x-δ,x+δ}]
  • 在 Around[s] 中，可用以下方式指定数字及其不确定度：
  • x （近似数）Around[x,(10^-Accuracy[x])/2]
    Interval[{xmin,xmax}]Around[(xmax+xmin)/2,(xmax-xmin)/2]
    dist （统计分布）Around[Mean[dist],StandardDeviation[dist]]
    list（元素列表）Around[Mean[list],StandardDeviation[list]]
    "nn.dddd" （数字字符串）（不确定性由有效数字的个数决定）
  • 对于线性计算，Around[x,δ] 就像一个数字，其值服从正态分布 NormalDistribution[x,δ].
  • Around 对象 Around[x1,δ1] 和 Around[x2,δ2] 上的关系运算符如 Less、Equal 和 Greater 会根据中心 x1 和 x2 的距离是大于还是小于 2 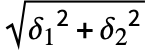的结果，来判断是否返回 True 或 False. 当与 Around 对象比较时，数字会被赋予零不确定性.
  • 当中心 x1、x2 的距离小于 0.5 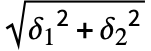时，NumericalOrder[Around[x1,δ1],Around[x2,δ2]] 返回 0. 否则根据中心的排序会返回 1 或 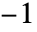. 与 Around 对象一起按数值进行排序时，数字会被赋予零不确定性.
  • 在 Around[x,δ] 中，值 x 和不确定度 δ 可以是任何数值表达式或符号表达式. 如果 δ 是数值表达式，那么 x 和 δ 将被数字化. 默认情况下，将使用机器精度，但如果需要准确表示数字，可以使用更高的精度.
  • Around[x,δ] 显示具有一位或两位数字的不确定度 δ；x 的小数点右边的位数与 δ 中所示的位数相同.
  • 在 Around[x,δ] 中，x 和 δ 可以是单位不同的量，但单位要互相兼容.
  • Around[{x1,x2,…},δ] 依次作用于第一个参数列表中的各项；视 xi 的各个不确定度为不相关.

范例

打开所有单元关闭所有单元

基本范例  (10)

大小不同、不确定度也不同的不确定的数字：

单位不同的不确定 Quantity 对象：

具有非对称不确定度的 Around 对象：

在输入中指定 5% 的相对不确定度：

用 Around 对象进行计算：

绘制 Around 对象组成的列表：

提取 Around 对象的部分内容：

同一个 Around 对象的两个不同实例被认为是不相关的：

因此，所得结果的不确定度小于乘以 2 所得的不确定度：

使用符号式 Around 对象：

对其进行计算：

将符号式 Around 对象相加，假定不确定度互不相关：

范围  (20)

不确定的对象  (6)

不确定的数字：

具有非对称不确定度的不确定数字：

不确定的 Quantity 对象：

数值和不确定度的单位相互兼容：

数值和不确定度的单位相同：

结果是一个 Quantity 对象，大小为 Around：

单位兼容的非对称的不确定度：

具有相同不确定度的大小不同的值：

不确定度大小不同的值：

具有 30% 相对不确定度的不确定数字：

用 Quantity 百分数表示同一个对象：

任意量纲的 Quantity 值：

访问器和转换  (4)

提取 Around 对象的值和不确定度：

根据 Around 对象构建有限精度数：

其准确度与 a 的不确定度相同：

根据有限精度数重建原来的 Around 对象：

构建以 Around 对象的值为中心的区间，半区间宽度为该对象的不准确度：

根据区间重建原来的 Around 对象：

用 Around 对含有数字的字符串进行转换，假设最后一位有效数字的不确定度为 0.5：

用不确定对象进行计算  (4)

用数字进行基本运算：

用 Quantity 对象进行基本运算：

构建一个 QuantityArray 对象，其中的元素为 Around 对象：

执行计算，保留 QuantityArray 结构：

归一化结果：

用符号式 Around 对象进行基本运算：

不确定对象的比较和排序  (6)

比较两个中心相距甚远的 Around 对象：

其距离显著大于零：

比较中心较近的 Around 对象：

其距离并不显著大于零：

比较有一个数字的 Around 对象：

距离显著大于零：

比较有 Quantity 中心和不确定性的 Around 对象：

它们之间的距离显著大于零：

对 Around 对象和数字集合进行数值排序：

对速度集合进行数值排序：

转换至共同的基本单位，以直接比较数值：

应用  (3)

绘制不确定的数据：

绘制系外行星的半径与质量，包括两个变量的不确定度：

计算质量和半径的平均值：

与地球的质量和半径进行比较：

使用值 作为地球重力，并假设这些量的最后一个有效位数为一个单位的不确定性，来计算长度为 的摆的振荡周期：

属性和关系  (3)

对 Around 对象取平方，使用一阶级数近似：

用 TransformedDistribution 进行相应的精确计算：

使用更高阶的级数展开式可以更好地逼近精确结果：

直接在非对称分布上使用 Around 会返回具有非对称不确定度的对象：

选择正态分布并进行模拟：

Around[scalars] 估计分布的均值和标准差：

Around[dist] 给出分布 dist 的真实参数：

MeanAround[scalars] 描述分布的均值和均值的标准误差：

Around[x,δ] 和 CenteredInterval[x,δ] 在数值运算中使用不同的传播规则：

Wolfram Research (2019)，Around，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Around.html （更新于 2023 年）.

文本

Wolfram Research (2019)，Around，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Around.html （更新于 2023 年）.

CMS

Wolfram 语言. 2019. "Around." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2023. https://reference.wolfram.com/language/ref/Around.html.

APA

Wolfram 语言. (2019). Around. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Around.html 年

BibTeX

@misc{reference.wolfram_2025_around, author="Wolfram Research", title="{Around}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/Around.html}", note=[Accessed: 03-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_around, organization={Wolfram Research}, title={Around}, year={2023}, url={https://reference.wolfram.com/language/ref/Around.html}, note=[Accessed: 03-April-2025 ]}