BandpassFilter

BandpassFilter[data,{ω1,ω2}]

カットオフ周波数が ω1と ω2のバンドパスフィルタをデータの配列に適用する．

BandpassFilter[data,{{ω,q}}]

中心周波数 ω，Q値 q を使う．

BandpassFilter[data,spec,n]

長さ n のフィルタカーネルを使う．

BandpassFilter[data,spec,n,wfun]

平滑化窓 wfun をフィルタカーネルに適用する．

詳細とオプション

  • バンドパスフィルタリングは．音声イコライザーや音声受信機で，信号内の中周波数は変更せずに低周波数と高周波数を減衰させるためにしばしば使用される．
  • BandpassFilterは，窓法で作成された有限インパルス応答 (FIR) カーネルを使用してデジタル信号をたたみ込みむ．
  • カーネルが長くなると周波数の識別が向上する．
  • data は次のいずれでもよい．
  • list任意階数の数値配列
    tseriesTimeSeriesやTemporalDataのような時間データ
    image任意のImageオブジェクトまたはImage3Dオブジェクト
    audioAudioオブジェクトまたはSoundオブジェクト
  • 減衰される周波数の範囲はカットオフ周波数 ω1および ω2 (ω2>ω1)に依存する．
  • 画像や多次元配列に適用された場合，フィルタリングはレベル1から始めて各次元に連続的に適用される．BandpassFilter[data,{{ω11,ω21},…}]は i 次元で周波数{ω1i,ω2i}を使う．
  • BandpassFilter[data,{ω1,ω2}]はカットオフ周波数{ω1,ω2}と入力 data に適したフィルタカーネル長と平滑化窓を使う．
  • よく使われる窓 wfun
  • BlackmanWindowBlackman窓で平滑化する
    DirichletWindow平滑化は行わない
    HammingWindowハミング窓で平滑化する
    {v1,v2,…}値 viの窓を使う
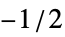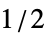    fからの範囲で f をサンプリングすることで窓を作る
  • 使用可能なオプション
  • Padding "Fixed"使用する充填値
    SampleRate Automatic入力に想定されるサンプルレート
  • デフォルトでデータと同様画像にもSampleRate->1が想定される．音声信号と時系列については，サンプルレートは抽出されるか入力データから計算されるかする．
  • SampleRatesr の場合，カットオフ周波数 ωcは 0から sr 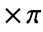まででなければならない．

例題

すべて開くすべて閉じる

例  (3)

余弦の和にバンドパスフィルタをかける：

音声のバンドパスフィルタをかける：

画像にバンドパスフィルタをかける：

スコープ  (13)

データ  (7)

1Dパルス列にフィルタをかける：

2Dパルス列にフィルタをかける：

TimeSeriesにフィルタをかける：

3全音信号のSoundオブジェクトにバンドパスフィルタをかける：

長さ101のBlackman窓でバンドパスフィルタを使って外側の音を除去する：

半音画像にバンドパスフィルタをかける：

3D画像にバンドパスフィルタをかける：

厳密精度を使ってフィルタをかける：

パラメータ  (6)

サンプルレート s の音声信号では，数値周波数は rad/s 数量として解釈される：

カットオフ周波数が8000Hzと12000Hzのバンドパスフィルタを使ってホワイトノイズ信号にフィルタをかける：

9798Hzの中心周波数と2のQ値 q を使う：

Q値を大きくすることでパスバンドを狭める：

長さ33のフィルタを使う：

より長いカーネルを使って周波数弁別を大きくする：

さまざまな窓関数を使って減衰量を変える：

調節可能なカイザー(Kaiser)窓を使って減衰量を変える：

数値リストとして窓関数を指定する：

さまざまな中心周波数を使ったバンドパスフィルタリング：

同じ中心周波数を使い，Q値を変える：

各次元で異なる中心周波数を使う：

オプション  (3)

Padding  (1)

充填法を変えるとエッジ効果も変わる：

SampleRate  (2)

サンプルレート sr=1を仮定して周波数 π/2に中心を置くフィルタを使う：

サンプルレート sr=3を仮定する：

ハーフバンド周波数を中心としたバンドパスフィルタをレート44100Hzでサンプリングされた音声に適用する：

アプリケーション  (1)

現代の88鍵のピアノでは，55番目のキー(C5)の基本周波数は約523Hzである．BandpassFilterを使って，以下の音声クリップにある基本波は保持しつつ，このキーのすべての倍音を効率的に削除する：

基本周波数(523Hz)を中心とした長さ63の狭いフィルタ(Q=3)を使う：

2つの音声クリップの周波数スペクトルを比較する：

特性と関係  (6)

0と π のカットオフ周波数を使ってもとの列を返す：

LeastSquaresFilterKernelおよびハミング窓を使ってバンドパスフィルタを作る：

BandpassFilterの結果と比較する：

長さ21のバンドパスフィルタのインパルス応答：

フィルタの振幅スペクトル：

平滑化窓なしでの長さ21のバンドパスフィルタのインパルス応答：

フィルタの振幅スペクトル：

バンドパスフィルタの周波数弁別はフィルタの長さが増すにつれて向上する：

インパルス応答の長さはフィルタの品質因子が大きくなるにつれて長くなる：

考えられる問題  (1)

PaddingNoneのとき，返される出力は入力より短い：

インタラクティブな例題  (1)

さまざまな中心周波数とQ値を使って画像にバンドパスフィルタをかける：

Wolfram Research (2012), BandpassFilter, Wolfram言語関数， https://reference.wolfram.com/language/ref/BandpassFilter.html （2017年に更新）.

テキスト

Wolfram Research (2012), BandpassFilter, Wolfram言語関数， https://reference.wolfram.com/language/ref/BandpassFilter.html （2017年に更新）.

CMS

Wolfram Language. 2012. "BandpassFilter." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/BandpassFilter.html.

APA

Wolfram Language. (2012). BandpassFilter. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BandpassFilter.html

BibTeX

@misc{reference.wolfram_2024_bandpassfilter, author="Wolfram Research", title="{BandpassFilter}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/BandpassFilter.html}", note=[Accessed: 24-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_bandpassfilter, organization={Wolfram Research}, title={BandpassFilter}, year={2017}, url={https://reference.wolfram.com/language/ref/BandpassFilter.html}, note=[Accessed: 24-November-2024 ]}