CoefficientArrays[polys,vars]
gives the arrays of coefficients of the variables vars in the polynomials polys.


CoefficientArrays
CoefficientArrays[polys,vars]
gives the arrays of coefficients of the variables vars in the polynomials polys.
Details and Options

- CoefficientArrays gives a list containing SparseArray objects, which can be converted to ordinary arrays using Normal.
- If CoefficientArrays[polys,vars] gives {m0,m1,m2,…}, then polys can be reconstructed as m0+m1.vars+m2.vars.vars+…. »
- Any element of polys of the form lhs==rhs is taken to correspond to the polynomial lhs-rhs. »
- CoefficientArrays[polys,{form1,form2,…}] takes all expressions in polys that match any of the formi to be variables.
- CoefficientArrays[polys] is equivalent to CoefficientArrays[polys,Variables[polys]].
- The length of the list CoefficientArrays[polys,vars] is one more than the total degree of polys.
- The mi are sparse arrays with ranks
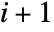 .
. - The first element m0 has the same length as the list polys.
- If polys is a single polynomial rather than a list, m0 is also not a list.
- For linear equations, the solution to Thread[polys==0] is given by LinearSolve[m1,-m0].
- For nonlinear equations, the mi are not unique. CoefficientArrays by default assigns nonzero coefficients only to monomials where the variables appear in the same order as vars.
- CoefficientArrays[polys,vars,"Symmetric"->True] makes all the mi symmetric in all their indices. The resulting arrays will generally be less sparse.
Examples
open all close allBasic Examples (1)
Scope (4)
Options (1)
"Symmetric" (1)
The default coefficient of a quadratic form corresponding to y x is zero:
With "Symmetric"->True, CoefficientArrays gives symmetric arrays:
Applications (1)
Convert linear equations to arrays suitable for LinearSolve:
Properties & Relations (3)
The polynomial can be reconstructed by using Dot (.):
The symmetric coefficient arrays correspond to vector derivatives at the origin:
CoefficientArrays gives a list of arrays of polynomial coefficients ordered by total degrees:
CoefficientList gives a tensor of the coefficients:
Use Coefficient to find the coefficient of ![]() :
:
In ca the position of this coefficient is a+b+1 followed by a 1s and b 2s (1 and 2 indicate the first and second variables):
In cl the coefficient of x^a y^b is the element at position {a+1,b+1}:
Tech Notes
Related Guides
History
Introduced in 2003 (5.0)
Text
Wolfram Research (2003), CoefficientArrays, Wolfram Language function, https://reference.wolfram.com/language/ref/CoefficientArrays.html.
CMS
Wolfram Language. 2003. "CoefficientArrays." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CoefficientArrays.html.
APA
Wolfram Language. (2003). CoefficientArrays. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CoefficientArrays.html
BibTeX
@misc{reference.wolfram_2025_coefficientarrays, author="Wolfram Research", title="{CoefficientArrays}", year="2003", howpublished="\url{https://reference.wolfram.com/language/ref/CoefficientArrays.html}", note=[Accessed: 14-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_coefficientarrays, organization={Wolfram Research}, title={CoefficientArrays}, year={2003}, url={https://reference.wolfram.com/language/ref/CoefficientArrays.html}, note=[Accessed: 14-January-2026]}