CoefficientArrays

CoefficientArrays[polys,vars]

多項式 polys の変数 vars の係数の配列を与える．

詳細とオプション

  • CoefficientArraysはSparseArrayオブジェクトを含むリストを与える．SparseArrayオブジェクトはNormalを使って通常の配列に変換することができる．
  • CoefficientArrays[polys,vars]が{m0,m1,m2,…}を与えるなら，polys をm0+m1.vars+m2.vars.vars+… として再構築することができる． »
  • lhs==rhs という形を持つ polys の要素はどれも多項式 lhs-rhs に対応すると取れる． »
  • CoefficientArrays[polys,{form1,form2,…}]はpolys 中の，formi のいずれかと一致するあらゆる式を変数と解釈する．
  • CoefficientArrays[polys]はCoefficientArrays[polys,Variables[polys]]と等価である．
  • リストCoefficientArrays[polys,vars]の長さは polys の全次数に1足したものと等価である．
  • mi は階数 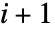の疎な配列である．
  • 最初の要素 m0 はリストpolys と同じ長さである．
  • polys がリストではなく1つの多項式である場合，m0 もまたリストではない．
  • 線形方程式の場合，Thread[polys==0]の解はLinearSolve[m1,-m0]で与えられる．
  • 非線形方程式の場合，mi は一意的ではない．デフォルトで，CoefficientArraysは変数が vars と同じ順序で現れる単項式にしか非零の係数を割り当てない．
  • CoefficientArrays[polys,vars,"Symmetric"->True]はすべての mi をすべての指標で左右対称にする．結果の配列は一般にそれほど疎ではなくなる．

例題

すべて開くすべて閉じる

例  (1)

スコープ  (4)

線形多項式：

線形多項式のリスト：

非線形多項式：

整方程式：

オプション  (1)

"Symmetric"  (1)

y x に対応する二次形式の係数のデフォルトは零である：

"Symmetric"->Trueとすると，CoefficientArraysは対称配列を返す：

アプリケーション  (1)

線形方程式をLinearSolveに適した配列に変換する：

特性と関係  (3)

多項式はDot (.)を使って再構成できる：

対称係数配列は原点におけるベクトル導関数に相当する：

CoefficientArraysは総次数で並べられた多項式係数の配列のリストを返す：

CoefficientListは係数のテンソルを返す：

Coefficientを使って の係数を求める：

caでは，この係数の位置は a 1と b 2が連結されて a+b+1となる（1と2は第1変数と第2変数を表す）：

clでは，x^a y^b の係数は位置{a+1,b+1}における要素である：

Wolfram Research (2003), CoefficientArrays, Wolfram言語関数， https://reference.wolfram.com/language/ref/CoefficientArrays.html.

テキスト

Wolfram Research (2003), CoefficientArrays, Wolfram言語関数， https://reference.wolfram.com/language/ref/CoefficientArrays.html.

CMS

Wolfram Language. 2003. "CoefficientArrays." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CoefficientArrays.html.

APA

Wolfram Language. (2003). CoefficientArrays. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CoefficientArrays.html

BibTeX

@misc{reference.wolfram_2024_coefficientarrays, author="Wolfram Research", title="{CoefficientArrays}", year="2003", howpublished="\url{https://reference.wolfram.com/language/ref/CoefficientArrays.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_coefficientarrays, organization={Wolfram Research}, title={CoefficientArrays}, year={2003}, url={https://reference.wolfram.com/language/ref/CoefficientArrays.html}, note=[Accessed: 21-November-2024 ]}