ConicOptimization

ConicOptimization[f,cons,vars]

錐制約 cons に従って線形目的関数 f の値を最小にする変数 vars の値を求める．

ConicOptimization[…,"prop"]

どの解の特性"prop"を返すべきかを指定する．

詳細とオプション

  • 錐最適化は，混合整数錐最適化，線形錐最適化あるいは線形錐計画法としても知られている．
  • 錐最適化は，線形最適化，線形分数最適化，二次最適化，二次錐最適化，半正定値最適化，幾何最適化等を含む，他の数多くの最適化の形式を含む．
  • 錐最適化は，実数，整数，複素数の変数で大域的に効率よく解くことができる凸最適化問題である．
  • 錐最適化は主問題を解く 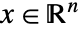を求める．
  • 最小化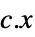
    制約条件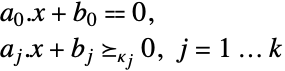
    ただし
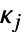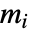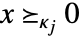  • 集合 は次元 の真凸錐でなければならない．次は，についてよく使われる錐指定と (VectorGreaterEqual[{x,0},κj]) に対応する集合である．
  • {"NonNegativeCone", m} 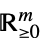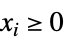となる
    {"NormCone", m}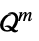TemplateBox[{{{, {{x, _, 1}, ,, ..., ,, {x, _, {(, {m, -, 1}, )}}}, }}}, Norm]<=x_mとなる
    {"SemidefiniteCone", m}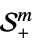対称半正定値行列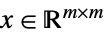
    "ExponentialCone"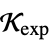となる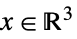
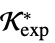
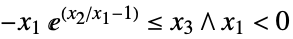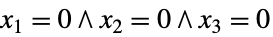    "DualExponentialCone"または となる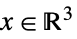
    {"PowerCone",α}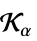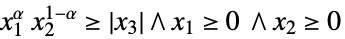となる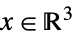
    {"DualPowerCone",α}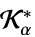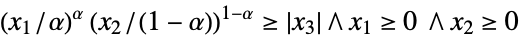となる
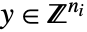  • 混合整数錐最適化は，問題を解く と を求める．
  • 最小化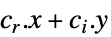
    制約条件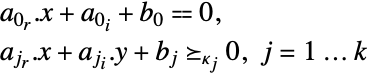
    ただし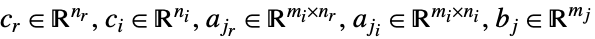
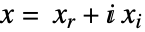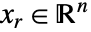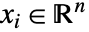  • ConicOptimizationは，目的関数が実数値のときは内部的に実変数 に変換することで x in TemplateBox[{}, Complexes]^nの問題を解く．ただし，で である．
  • 変数指定 vars は，次のいずれかの形式で変数を与える要素のリストでなければならない．
  • v名前が 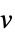で次元が推測される変数
    v∈Reals実数のスカラー変数
    v∈Integers整数のスカラー変数
    v∈Complexes複素数のスカラー変数
    v∈ℛ幾何学領域 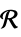に制限されたベクトル変数
    v∈Vectors[n,dom]または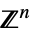のベクトル変数
    v∈Matrices[{m,n},dom]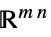またはの行列変数
  • 制約条件 cons は以下で指定できる．
  • LessEqualスカラー不等式
    GreaterEqual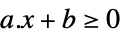スカラー不等式
    VectorLessEqual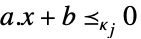ベクトル不等式
    VectorGreaterEqual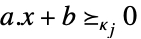ベクトル不等式
    Equal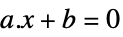スカラー等式またはベクトル等式
    Element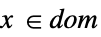凸領域または領域要素
  • ConicOptimization[f,cons,vars]のとき，parval（par は vars には含まれず，val は数値または数値配列）の形式のパラメータ方程式を制約条件に含めて，f あるいは cons で使われるパラメータを定義することができる． »
  • 主最小化問題は，関連する最大化問題（ラグランジュの双対問題）を有する．双対の最大値は，常に主最小値以下であるので，下限を与える．双対マキシマイザは，最小値の制約条件の変化に対する感度を含む主問題についての情報を与える． »
  • 錐最適化は次の双対問題を持つ． »
  • 最大化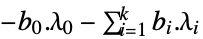
    制約条件
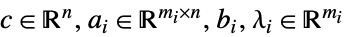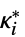    ただしおよび は 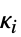の双対錐である
  • 次は，可能な解の特性"prop" である． »
  • "PrimalMinimizer" 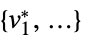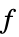を最小化する変数値のリスト
    "PrimalMinimizerRules" 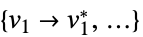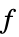を最小化する変数の値 vars={v1,…}
    "PrimalMinimizerVector" 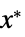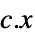を最小化するベクトル
    "PrimalMinimumValue"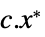最小値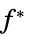
    "DualMaximizer"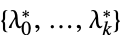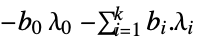を最大化するベクトル
    "DualMaximumValue"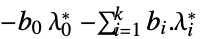双対最大値
    "DualityGap"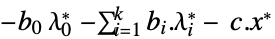双対最適値と主最適値の差
    "Slack"不等式制約を等式に変換するベクトル
    "ConstraintSensitivity"
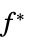    		の制約の摂動に対する感度
    "ObjectiveVector"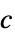線形目的ベクトル
    "ConicConstraints" 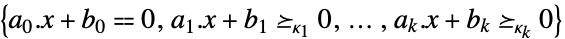標準形式の錐制約のリスト
    "ConicConstraintConeSpecifications" 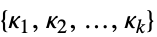錐体 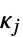についての指定のリスト
    "ConicConstraintConeDimensions"{TemplateBox[{Dimensions, paclet:ref/Dimensions}, RefLink, BaseStyle -> {3ColumnTableMod}][kappa_1],...}錐制約中の錐体の次元のリスト
    "ConicConstraintAffineLists" 錐制約中のアフィン変換のための行列とベクトル対のリスト
    {"prop1","prop2",…} いくつかの解の特性
  • 次は，使用可能なオプションである．
  • MaxIterationsAutomatic使用する最大反復回数
    Method Automatic使用するメソッド
    PerformanceGoal $PerformanceGoal最適化しようとするパフォーマンスの局面
    Tolerance Automatic内部比較に使用する許容度
  • オプションMethod->method を使って使用するメソッドを指定することができる．以下は，使用可能なメソッドである．
  • Automaticメソッドを自動的に選択する
    "SCS"SCS（錐ソルバの分割）ライブラリ
    "CSDP"CSDP（COIN半定値計画）ライブラリ
    "DSDP"DSDP（半定値計画）ライブラリ
    "MOSEK"商用MOSEK凸最適化ソルバ
    "Gurobi"商用Gurobi線形・二次最適化ソルバ
    "Xpress"商用Xpress線形・二次最適化ソルバ
  • 計算はMachinePrecisionに限られる．

例題

すべて開くすべて閉じる

例  (3)

二次元"NormCone"上で を最小化する：

最適点は，制約条件で定義された領域内で が最小となる点である：

三角形 と円板 の交点でを最小化する：

最小化点の位置を可視化する：

制約条件TemplateBox[{{{, {x, ,, y}, }}}, Norm]<=1,x in Z,y in Rに従って を最小化する：

スコープ  (35)

基本的な用法  (11)

制約条件 に従って を最小化する：

線形不等式制約の中にはVectorGreaterEqualで表せるものがある：

v>= または \[VectorGreaterEqual]を使ってベクトル不等式記号 を入力する：

スカラー不等式を使った同等の形：

ベクトル変数 を使う：

への縫込みがあるかもしれないので，不等式 は とは等しくないかもしれない：

への意図しない縫込みを避けるためにInactive[Plus]を使う：

定数パラメトリック方程式を使って意図しない への縫込みを避ける：

VectorGreaterEqualは"NonNegativeCone"についての錐不等式を表す：

錐の次元を明示的に指定するために{"NonNegativeCone",n}を使う：

解を求める：

制約条件 に従って を最小化する：

"NormCone"の錐不等式を使って制約条件 を指定する：

解を求める：

半正定値行列制約(x 1; 1 y)_(TemplateBox[{2}, SemidefiniteConeList])0に従って を最小化する：

解を求める：

ベクトル変数 とIndexed[x,i]を使って個々の成分を指定する：

あいまいなときは，Vectors[n]を使ってベクトル変数の次元を指定する：

NonNegativeReals ()を使って非負の制約条件を指定する：

ベクトル不等式 を使った同等の形：

整数変数  (4)

Integersを使って整数領域制約を指定する：

Vectors[n,Integers]を使ってベクトル変数についての整数領域制約を指定する：

NonNegativeIntegers ()を使って非負の整数領域制約を指定する：

NonPositiveIntegers ()を使って非正の整数領域制約を指定する：

複素変数  (5)

Complexesを使って複素変数を指定する：

実目的関数を複素変数と複素制約条件 で最小化する：

であるとする．制約条件を実数成分に展開すると以下が与えられる：

実数値の目的関数と複素変数および制約条件で問題を解く：

同じ問題を実変数と制約条件で解く：

二次制約 をエルミート行列 および実数値の変数と一緒に使う：

制約条件 でエルミート行列 と複素変数を使う：

線形行列不等式制約条件 a_(0)+a_(1) x_(1)+a_(2) x_(2)>=_(TemplateBox[{2}, SemidefiniteConeList])0をエルミート行列または対称行列と一緒に使う：

和がエルミート行列のままであるためには，線形行列不等式の変数は実数でなければならない：

主モデルの特性  (4)

三角形 と円板 の交点でを最小化する：

主ミニマイザをベクトルとして得る：

最小値を得る：

解をプロットする：

目的ベクトルを抽出する：

錐制約を抽出する：

錐制約内の錐指定 を抽出する：

錐制約内の錐次元 を抽出する：

錐制約内のアフィンリストを抽出する：

ミニマイザ における不等式 のスラックは で与えられる：

ミニマイザと錐制約のアフィンリストを抽出する：

スラックが aj.x*+bj-sj=0で s={s0,…,sk}を満足することを確認する：

標準形式の錐最適化問題は，およびに従って を最小化すると定義されることがある．標準形式に変換するために，各錐制約 について，変数 と対応する線形等式制約 を加える：

目的ベクトル，錐制約アフィンリスト，錐指定を抽出する：

スラック制約 は と同じである：

線形等式制約 を形成する：

変換された標準形式の錐問題を解く：

"Slack"特性によって，実際の変換を行わずに の値を得ることができる：

双対モデルの特性  (3)

と に従って を最小化する：

双対問題は，に従ってを最大化する：

強双対性のため，主最小値と双対最大値は一致する：

これは，0の双対性ギャップを持つことに等しい．一般に，最適点で である：

主問題から抽出した係数を使って双対問題を構築する：

目的ベクトルと制約アフィンリストを抽出する：

と を得る：

双対問題は，に従ってを最大化する：

解の特性を使って双対最大値と双対マキシマイザを直接得る：

"DualMaximizer"は以下で与えられる：

双対マキシマイザベクトル区分は双対錐の数と次元にマッチする：

感度特性  (3)

制約条件の摂動による最適値の変化を求める：

"ConstraintSensitivity"を計算する：

新たな制約条件t a.{x,y}+b+delta_(TemplateBox[{3}, NormConeList])0について考える．ただし， は摂動である：

新たな最適値は以下であると推定できる：

摂動問題を直接解くことと比較する：

最適値は感度要素の符号に従って変化する：

感度要素が負の位置にあると，正の摂動が最適値を減少させる：

感度要素が正の位置にあると，正の摂動が最適値を増大させる：

制約条件の感度は双対マキシマイザの否定としても得ることができる：

サポートされる凸錐  (5)

"NonNegativeCone"  (1)

正九角形上で を最小化する：

目的関数のプロット上でミニマイザを示す：

錐制約に使われた錐を示す：

"NormCone"  (1)

円板上で を最小化する：

目的関数のプロット上でミニマイザを示す：

錐制約に使われた錐を示す：

"SemidefiniteCone"  (1)

が半正定値になるように を最小化する：

目的関数のプロット上でミニマイザを示す：

錐制約に使われた錐を示す：

"ExponentialCone"  (1)

制約条件 に従って を最小化する：

目的関数のプロット上にミニマイザを示す：

錐制約に使われた錐を示す：

"PowerCone"  (1)

4ノルムの単位円板上で を最小化する：

目的関数のプロット上でミニマイザを示す：

錐制約に使われた錐を示す：

オプション  (11)

Method  (8)

"SCS"は，分割錐ソルバ法を使う：

"CSDP"は，半定値問題についての内点法である：

"DSDP"は，半定値問題についての別の内点法である：

"IPOPT"は，非線形問題についての内点法である：

メソッドによってデフォルトの許容度が異なり，それが確度と精度に影響する：

厳密解と近似解を計算する：

"SCS"のデフォルトの許容度はである：

"CSDP"，"DSDP"，"IPOPT"のデフォルトの許容度はである：

"SCS"法は，指定されるとSCSライブラリのデフォルト許容度である10-3で呼び出される：

デフォルトオプションだと，この問題は"SCS"法を使って許容度10-6で解かれる：

"CSDP"法または"DSDP"法を半定値制約条件まで使う：

"CSDP"法を使って問題を解く：

"DSDP"法を使って問題を解く：

"CSDP"あるいは "DSDP"が適用できない場合は，"IPOPT"法を使って正確な解を得る．制約条件を指定する：

"IPOPT"は，"SCS"より正確な結果を生成するが，速度は遅くなることが多い：

かかった時間を"SCS"法と比較する：

PerformanceGoal  (1)

オプションPerformanceGoalのデフォルト値は$PerformanceGoalである：

PerformanceGoal"Quality"を使ってより確度の高い結果を得る：

PerformanceGoal"Speed"を使って，品質を犠牲にして結果を速く得る：

かかった時間を比較する：

"Speed"を目標にすると結果があまり正確ではなくなる：

Tolerance  (2)

Toleranceの設定を小さくするとより正確な結果が与えられる：

Minimizeで厳密な最小値を計算する：

Toleranceの設定を変えて最小値における誤差を計算する：

許容度における最小値誤差の変化を可視化する：

Toleranceの設定を小さくするとより正確な答が得られるが，計算時間が長くなるかもしれない：

許容度を小さくすると，より時間がかかる：

許容範囲を狭めると，より正確な答が与えられる：

アプリケーション  (29)

基本的なモデリング変換  (13)

に従って を最小化する．目的関数を否定することで最大化問題を解く：

主最小値を否定して対応する最大値を得る：

を中心とする半径の円板上でを最小化する． に等しい追加的な制約 を加えて目的関数を線形関数 に変換する：

円板制約もまたNormを使って表すことができる：

正五角形上でを最小化する．と追加的な制約条件を使って目的関数を線形関数に変換する：

を最小化する．補助変数 を使うと，目的は制約条件 に従って を最小化することに変わる：

に従ってを最小化する．2つの補助変数 と を使って，に従って を最小化するように問題を変換する：

を最小化する．補助変数 を使い， に従って を最小化するように問題を変換する：

を最小化する代りに に従って を最小化する．ただし， は非減少関数である．主ミニマイザ はどちらの問題でも同じである．に従って を最小化することを考える：

真の最小値は， の最小値に を適用すると得られる：

を中心とする半径の円板上で を最小化する．補助変数 を使うと，目的は追加の制約 を持つ を最小化することに変わる：

制約条件 は，{t,1,x+y}_(TemplateBox[{}, ExponentialConeString])0のときかつそのときに限り，指数錐制約 に等しい：

を中心とした半径の円板上でTemplateBox[{{x, +, y}}, Abs]^(1.5)を最小化する．制約条件TemplateBox[{{x, +, , y}}, Abs]^(1.5)<=t に従って を最小化するように補助変数 を使って問題を変換する：

制約条件 TemplateBox[{{x, +, , y}}, Abs]^(1.5)<=t は TemplateBox[{{x, +, y}}, Abs]<=t^((1/1.5))<==> TemplateBox[{{x, +, y}}, Abs]<=t^((1/1.5))1^((1-1/1.5))に等しい．これは，"PowerCone" を使った {t,1,x+y}_(TemplateBox[{{1, /, 1.5}}, PowerConeList])0で表すことができる：

を最小化する を求める：

補助変数 を使って，制約条件 に従って を最小化するように問題を変換する：

これは，"PowerCone"制約条件を使って表すことができる．sum_(i=1)^n(TemplateBox[{{{{a, _, i}, x}, -, {b, _, i}}}, Abs]^(1.5))/(t^(1.5-1))<=t のときかつそのときに限り||a.x-b||_(1.5)= (sum_(i=1)^nTemplateBox[{{{{a, _, i}, x}, -, {b, _, i}}}, Abs]^(1.5))^(1/1.5)<=t なので，を(TemplateBox[{{{{a, _, i}, x}, -, {b, _, i}}}, Abs]^(1.5))/(t^(1.5-1))の境界とする．ただし， は{s_i,t,a_ix-b_i}_(TemplateBox[{{1, /, 1.5}}, PowerConeList])0, i=1,...,n を与えるものとする：

決定変数, に線形依存する対称行列の最大固有値を最小化するを求める．は と等価なので，この問題は線形行列不等式として立式できる．ただし， は の 番目の固有値である．線形行列関数 を定義する：

実対称行列 は直交行列 で対角化可能なので ．したがって，のときかつそのときに限り．任意の は を取って ．したがて，のときかつそのときに限り ．数値的にシミュレーションを行なってこれらの式が等しいことを示す：

結果の問題：

モンテカルロシミュレーションを行なって結果の妥当性をチェックする：

に従い，のとき を仮定して を最小化する．補助変数 を使って となるように を最小化することが目的となる：

が を含意することをチェックする：

シューアの補題における制約条件は，のときかつそのときに限り，であればブロック行列であるとする．したがって，のときかつそのときに限り である．Inactive Plusを使って縫込みを回避するための条件を構築する：

楕円体，二次錐，放物体を含む二次集合 について，かどうかを判断する．ただし，は対称行列，はベクトル，はスカラーである：

集合 iが全次元であると仮定すると，S-procedureは，となるような非負の数 が存在するときかつそのときに限りであるとする．非負の数 が存在することを視覚的に確かめる：

λ≥0なので，となる：

データフィッティング問題  (5)

制約条件 に従って を最小化する：

補助変数 を使うと，目的は， に従って を最小化することに変わる：

データの最初と最後の点が曲線上に来るように，三次曲線を離散データをフィットする：

DesignMatrixを使って行列を構築する：

最初と最後の点が曲線上に来るように条件を定義する：

を最小化して係数 を求める．補助変数 を使うと，目的は に従って を最小化することに変わる：

データとフィットを比較する：

を最小化することで，非線形離散データの強力なフィットを求める：

基底 を使ってデータをフィットする．補間関数は である：

なので，補助変数 を使う．問題は変形されて，制約条件 に従って を最小化することになる：

フィットを可視化する：

補間関数と基準関数を比較する：

与えられた多項式 を平方和多項式によって表す：

目的は，となるような を求めることである．ただし，は単項式のベクトルである：

対称行列 を構築する：

多項式 と の係数を求め，両者が等しいことを確かめる：

の要素を求める：

二次の項 ．ただし， は のコレスキー分解で得られた下三角行列である：

平方和多項式と与えられた多項式を比較する：

複素 について||a.lambda-b||+sigma TemplateBox[{lambda, 1}, Norm2]を最小化することで複素データの正規化フィットを求める：

DesignMatrixを使って基底について行列 を構築する：

係数 を求める：

が の実成分と複素成分の関数として定義されたフィットであるとする：

の実成分についての結果を可視化する：

の複素成分についての結果を可視化する：

幾何問題  (5)

と を中心とする半径1の2枚の円板の最短距離を求める．は円板1の上の点，は円板2の上の点とする．目的は，を最小化することである．補助変数 を使うと目的はに従って を最小化することに変わる：

2点の位置を可視化する：

補助変数 は2点間の距離を与える：

指定された領域を囲い込んでいる，半径 で中心が の最小の球を求める：

制約条件 に従って半径 を最小化する：

囲い込んでいる球を可視化する：

囲い込んでいる最小の球はBoundingRegionを使って効率的に求められる：

交差していない2つの凸多角形を分ける平面を求める：

は 上の点，は 上の点だとする．目的は，を最小にすることである．補助変数 を使うと，目的はに従って を最小にすることに変わる：

分離超平面定理によると，制約条件 に関連付けられた双対は超平面の法線を与えるという：

以下は，"NormCone"に関連付けられた双対である：

超平面は以下のように構築される：

2つの多角形を分ける平面を可視化する：

凸多角形にフィットすることができる，としてパラメータ化された最大面積の楕円を求める：

凸多角形の各線分は半平面 の交点として表すことができる．線形不等式を抽出する：

半平面にパラメータ化を適用すると，が与えられる．項はである．したがって制約条件はである：

面積の最小化は の最小化に等しい．これはの最小化に等しい：

パラメータ化された楕円をとして明示的な形に変換する：

凸多角形の解析的中心を求める．解析的中心は制約条件までの距離の積を最大にする点である：

凸多角形の各線分は半平面 の交点として表すことができる．線形不等式を抽出する：

目的はを最小化することである．を取って目的関数を否定する．目的はに変わる：

補助変数 を使って変形された目的は，制約条件 に従って を最小化することである：

中心の位置を可視化する：

分類問題  (3)

2つの点集合 と を分離する直線 を求める：

分離するためには，集合1は を，集合2は を満足しなければならない：

目的は，と の間の厚みの2倍を与えるを最小化することである．補助変数 を使うと，目的は制約条件 に変わる：

分離線は次のようになる：

三次元の点の2つの集合 と を分ける二次多項式を求める：

DesignMatrixを使って，2つの集合のための二次多項式データ行列を構築する：

分離するためには，集合1は を，集合2は を満足しなければならない：

を最小化することで分離多項式を求める．補助変数 を使うと，変形された目的は追加的な制約条件 に従って を最小化することになる：

2つの点集合を分離する多項式：

2つのデータ集合を分離する多項式をプロットする：

与えられた点の集合 を別の集合に分割する．これは，を最小化することで，各集合の中心 を求めることによってなされる．ただし，は与えられたローカルカーネルであり は与えられたペナルティパラメータである：

カーネル は，もし ならば ，それ以外では の 最近傍()関数である．この問題のために 最近傍が選ばれた：

補助変数 を使うと，目的は制約条件 に従って を最小化することに変わる：

集合の中心を求める：

各データ点に対応する中心が存在する．同じ集合に属するデータは同じ中心を持つ：

グループ化された点を抽出してプロットする：

最適制御問題  (1)

，，に従って を最小化する：

最小化関数積分は台形規則を使って近似できる．離散化された目的関数は，追加的な条件 に従って になる：

の時間導関数は階差を使って離散化される：

初期条件の制約 はIndexedを使って指定できる：

補助変数 を使って， に従って を最小化するように目的変数が変換された：

離散化された結果をInterpolatingFunctionに変換する：

制御変数をプロットする：

状態変数をプロットする．状態変数は関数 を追跡しようとする：

施設配置問題  (1)

さまざまな携帯電話の基地局 の位置と にいるクライアントにサービスを届けるために必要な範囲 を求める：

各基地局は，で与えられるその範囲に比例して電力を消費する．目的は電力消費を最小にすることである：

を，基地局 でクライアント がカバーされるならば　であることを示す決定変数とする：

各基地局は，その範囲でクライアントのある部分をカバーする位置になければならない：

各基地局は複数のクライアントをカバーすることができる：

各基地局は最小と最大のカバレッジを持つ：

すべての変数をまとめる：

基地局の位置とその範囲を求める：

基地局の位置と範囲を抽出する：

クライアントの場所に対する基地局の位置と範囲を可視化する：

ポートフォリオの最適化  (1)

リスクが最小でリターンか最大になるような，資本 の6つの株式への投資配分を求める：

リターンは で与えられる．ただし， は個別の株式の予想収益の値のベクトルである：

リスクは で与えられる． はリスク回避パラメータであり， である：

目標は，指定されたリスク回避パラメータについてリスクを最小にしつつリターンを最大にすることである：

株式の売買による株式の市場価格はでモデル化される．これは，エピグラフ変換を使ったPower Coneによってモデル化できる：

重み はどれも0より大きくなければならず，重みに市場影響コストを加えたものは1でなければならない：

リスク回避パラメータの範囲について，利益と対応するリスクを計算する：

範囲 での最適な は，リスクとリターンのトレードオフの上界包絡線を与える：

指定数のリスク回避パラメータについて重みを計算する：

市場コストを計上することで，低リスク回避のための多様化したポートフォリオが得られるが，リスク回避が高い場合は，多様化されていない株式を購入するため，市場への影響コストが支配的になる：

特性と関係  (8)

ConicOptimizationは目的関数の大域的最小値を与える：

実行可能領域上の最小値を用いて目的関数をプロットする：

Minimizeは錐問題についての大域的厳密結果を与える：

NMinimizeを使って，大域メソッドを使った近似結果を得ることができる：

FindMinimumを使って，局所メソッドを使った近似結果を得ることができる：

SemidefiniteOptimizationはConicOptimizationの特殊ケースである：

SecondOrderConeOptimizationはConicOptimizationの特殊ケースである：

QuadraticOptimizationは ConicOptimizationの特殊ケースである：

補助変数 を使い，追加的な制約条件 で を最小化する：

LinearOptimizationはConicOptimizationの特殊ケースである：

考えられる問題  (6)

最適点における制約条件はある程度の許容度まで満足するものと期待される：

制約条件違反はしばしばToleranceオプションで制御される：

空集合あるいは実行不可能な問題の最小値はであると定義される：

ミニマイザはIndeterminateである：

非有界集合あるいは非有界問題の最小値はである：

ミニマイザはIndeterminateである：

下手にスケールされた問題の結果は大きい誤差を含む可能性がある：

正しい結果は以下の通りである：

を10-10でスケールした後では，以下の問題と数学的に等しくなる：

5*10-10の±10-6の範囲での と についての任意の結果は許容度10-6の範囲に収まり，スケールバックした際の誤差は最大で以下のようになる：

前のスケールされた問題を解くことも，デフォルトの許容度をより小さくすることもできる：

混合整数問題についての双対に関連した解の特性は得られないかもしれない：

複素値を含む制約条件はベクトル不等式で指定しなければならない：

Lessを使うだけでは，理論的に両辺が実数であってもうまくいかない：

Wolfram Research (2019), ConicOptimization, Wolfram言語関数， https://reference.wolfram.com/language/ref/ConicOptimization.html （2020年に更新）.

テキスト

Wolfram Research (2019), ConicOptimization, Wolfram言語関数， https://reference.wolfram.com/language/ref/ConicOptimization.html （2020年に更新）.

CMS

Wolfram Language. 2019. "ConicOptimization." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/ConicOptimization.html.

APA

Wolfram Language. (2019). ConicOptimization. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ConicOptimization.html

BibTeX

@misc{reference.wolfram_2024_conicoptimization, author="Wolfram Research", title="{ConicOptimization}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/ConicOptimization.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_conicoptimization, organization={Wolfram Research}, title={ConicOptimization}, year={2020}, url={https://reference.wolfram.com/language/ref/ConicOptimization.html}, note=[Accessed: 21-November-2024 ]}