Convolve

Convolve[f,g,x,y]

式 fと g の x についてのたたみ込みを返す．

Convolve[f,g,{x1,x2,…},{y1,y2,…}]

多次元たたみ込みを返す．

詳細とオプション

  • Convolveは，フーリエ(Fourier)たたみ込み，非因果的たたみ込み，両側たたみ込みとしても知られている．
  • 2つの関数 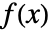と 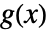のたたみ込み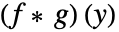は 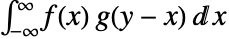で与えられる．
  • 多次元たたみ込みは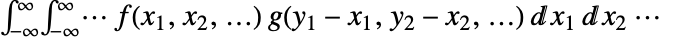で与えられる．
  • 使用可能なオプション
  • Assumptions $Assumptionsパラメータに関する仮定
    GenerateConditions Falseパラメータについての条件を生成するかどうか
    MethodAutomatic使用するメソッド
    PrincipalValueFalse初期値積分を使うかどうか

例題

すべて開くすべて閉じる

例  (3)

DiracDeltaで関数をたたみ込む：

2つの単位パルスをたたみ込む：

2つの指数関数をたたみ込んで結果をプロットする：

スコープ  (5)

一変数のたたみ込み  (3)

このたたみ込みは平行移動の積積分を与える：

初等関数：

たたみ込みは一般に関数を滑らかにする：

この族に関しては，すべてが単位面積を持つ：

多変数のたたみ込み  (2)

このたたみ込みは平行移動の積積分を与える：

多変数デルタ関数のたたみ込みは点演算子として動作する：

有界サポートを持つ関数のたたみ込みはフィルタとして動作する：

一般化と拡張  (1)

UnitStepによる乗算は，事実上有限区間におけるたたみ込みを返す：

オプション  (2)

Assumptions  (1)

変数すなわちパラメータについての仮定を指定する：

GenerateConditions  (1)

パラメータの範囲についての条件を生成する：

アプリケーション  (5)

たたみ込みを使って線形常微分方程式の特殊解を得る：

インパルス応答が h のときの線形で時不変系のステップ応答を得る：

系のステップ応答：

UniformDistributionのPDFのそれ自身でのたたみ込みはTriangularDistributionを与える：

UniformSumDistribution[n]は n 個のUniformDistribution[]の確率密度関数のたたみ込みである：

ErlangDistribution[k,λ]は k 個のExponentialDistribution[λ]の確率密度関数のたたみ込みである：

特性と関係  (7)

Convolveは数直線上で積分を計算する：

DiracDeltaを伴うたたみ込みは関数自身を与える：

スケーリング：

交換性：

分配性：

因果的たたみ込みのラプラス(Laplace)変換は個々の変換の積である：

たたみ込みのフーリエ(Fourier)変換は個々の変換の積に関連している：

インタラクティブな例題  (1)

以下はたたみ込み演算を示す：

Wolfram Research (2008), Convolve, Wolfram言語関数， https://reference.wolfram.com/language/ref/Convolve.html.

テキスト

Wolfram Research (2008), Convolve, Wolfram言語関数， https://reference.wolfram.com/language/ref/Convolve.html.

CMS

Wolfram Language. 2008. "Convolve." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Convolve.html.

APA

Wolfram Language. (2008). Convolve. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Convolve.html

BibTeX

@misc{reference.wolfram_2024_convolve, author="Wolfram Research", title="{Convolve}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/Convolve.html}", note=[Accessed: 15-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_convolve, organization={Wolfram Research}, title={Convolve}, year={2008}, url={https://reference.wolfram.com/language/ref/Convolve.html}, note=[Accessed: 15-November-2024 ]}