EccentricityCentrality

EccentricityCentrality[g]

グラフ g 中の頂点の離心中心性のリストを与える．

EccentricityCentrality[{vw,…}]

規則 vw を使ってグラフ g を指定する．

詳細

  • EccentricityCentralityは，到達可能な他のどの頂点とも最大距離が短い頂点に高い中心性を与える．
  • グラフ g のEccentricityCentralityは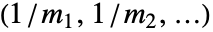で与えられる．ただし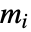， は頂点 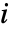に連結している他のすべての頂点への，頂点 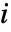からの最大距離である．
  • 孤立した頂点の離心中心性は0であるとみなされる．
  • EccentricityCentralityは，無向グラフ，有向グラフ，重み付きグラフ，多重グラフ，混合グラフに使うことができる．

予備知識

  • EccentricityCentralityは，グラフ頂点の特定の中心性を近似する非負の機械数（離心中心性）のリストを返す．離心中心性は，ノード 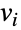から他のすべての到達可能なノードまでの最大距離が短いこと（つまり，グラフの離心率）に基づいた，ネットワーク中のノードの中心性の尺度である．この尺度はソーシャルネットワーク，交通，生物学，社会科学等に応用されている．
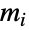  • が頂点 から に接続している他のすべての頂点への最大距離である場合，離心中心性は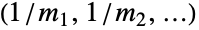で与えられる．孤立頂点の離心中心性は0であると解釈される．離心中心性は0から1の間にある（0と1は含まれる）．
  • 頂点の離心中心性はその頂点のVertexEccentricityの逆数である．グラフの完全距離行列はGraphDistanceMatrixを使って計算することができる．

例題

すべて開くすべて閉じる

例  (2)

離心中心性を計算する：

ハイライトする：

頂点に順位を付ける．順位が最も高い頂点は，到達可能な他のどの頂点とも近距離にある頂点である：

スコープ  (7)

EccentricityCentralityは無向グラフに使うことができる：

有向グラフに使うこともできる：

重み付きのグラフに使う：

多重グラフ：

混合グラフ：

規則を使ってグラフを指定する：

EccentricityCentralityは大きいグラフに使うことができる：

アプリケーション  (5)

離心性によって頂点に順位を付ける：

CycleGraphの離心中心性をハイライトする：

GridGraph：

CompleteKaryTree：

PathGraph：

ミクロネシア諸島の東に位置するマーシャル諸島のインフラストラクチャーネットワークに基づいて，戦略的に位置付けられた島を求める：

これはグラフの中央値によって変わる：

シカゴ郊外を結ぶ道路網から，救急車両の走行距離を最短にする病院と消防署の位置を求める：

個の頂点を持つグラフの場合，最も中心的な頂点と他のすべての頂点との間の離心中心性における差の最大総和はの逆数である：

最も中心にある頂点がどのくらい中心にあるか，他の頂点との関係から測る：

ソーシャルネットワークの集中化：

特性と関係  (6)

EccentricityCentralityは他の到達可能な頂点への最大距離の逆数である：

他の到達可能な頂点までの最大距離の逆数：

頂点の離心中心性はVertexEccentricityの逆数である：

離心中心性は0から1までである：

無向グラフの離心中心性は各成分の中心性に等しい：

各成分の中心性を計算しても同じ結果が得られる：

GraphCenterを使って離心中心性が最も高い頂点を求める：

VertexIndexを使って特定の頂点の中心性を求める：

Wolfram Research (2012), EccentricityCentrality, Wolfram言語関数， https://reference.wolfram.com/language/ref/EccentricityCentrality.html （2015年に更新）.

テキスト

Wolfram Research (2012), EccentricityCentrality, Wolfram言語関数， https://reference.wolfram.com/language/ref/EccentricityCentrality.html （2015年に更新）.

CMS

Wolfram Language. 2012. "EccentricityCentrality." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/EccentricityCentrality.html.

APA

Wolfram Language. (2012). EccentricityCentrality. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EccentricityCentrality.html

BibTeX

@misc{reference.wolfram_2024_eccentricitycentrality, author="Wolfram Research", title="{EccentricityCentrality}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/EccentricityCentrality.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_eccentricitycentrality, organization={Wolfram Research}, title={EccentricityCentrality}, year={2015}, url={https://reference.wolfram.com/language/ref/EccentricityCentrality.html}, note=[Accessed: 21-November-2024 ]}