Element[x,dom]
or x∈dom asserts that x is an element of the domain dom.
Element[x,reg]
or x∈reg asserts that x is an element of the region reg.
Element[x1|x2|…,dom]
asserts that all the xi are elements of dom.
Element[patt,dom]
asserts that any expression matching the pattern patt is an element of dom.


Element 
Element[x,dom]
or x∈dom asserts that x is an element of the domain dom.
Element[x,reg]
or x∈reg asserts that x is an element of the region reg.
Element[x1|x2|…,dom]
asserts that all the xi are elements of dom.
Element[patt,dom]
asserts that any expression matching the pattern patt is an element of dom.
Details
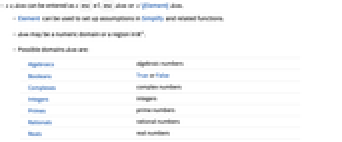
- x∈dom can be entered as x
 el
el dom or x \[Element] dom.
dom or x \[Element] dom. - Element can be used to set up assumptions in Simplify and related functions.
- dom may be a numeric domain or a region in
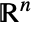 .
. - Possible domains dom are:
-
Algebraics algebraic numbers Booleans True or False Complexes complex numbers Integers integers Primes prime numbers Rationals rational numbers Reals real numbers - Possible regions reg are defined by RegionQ.
- x∈dom if possible evaluates immediately when x is numeric.
- For a domain dom, {x1,x2,…}∈dom is equivalent to (x1|x2|…)∈dom.
- For a region reg, {x1,x2,…}∈reg asserts that the point with coordinates x1,x2,… belongs to reg.
- {x1,x2,…}∈dom evaluates to (x1|x2|…)∈dom if its truth or falsity cannot immediately be determined.
Examples
open all close allBasic Examples (5)
Scope (9)
Make domain membership assumptions:
Test domain membership using assumptions:
Test region membership using assumptions:
Specify assumptions on objects matching a pattern:
TraditionalForm formatting:
Properties & Relations (2)
For a single variable, the negation of Element is automatically converted to NotElement:
For multiple variables, the negation of Element is not automatically simplified:
Use LogicalExpand to find the representation in terms of NotElement:
Element asserts region membership:
RegionMember gives explicit region membership conditions:
Possible Issues (1)
When domain membership cannot be decided the Element statement remains unevaluated:
See Also
Simplify MemberQ IntegerQ Assumptions Condition PatternTest Equal Less Divisible CoprimeQ Booleans Primes Exists ForAll Distributed GeometricScene
Characters: \[Element]
Tech Notes
Related Links
History
Introduced in 1999 (4.0) | Updated in 2003 (5.0) ▪ 2014 (10.0)
Text
Wolfram Research (1999), Element, Wolfram Language function, https://reference.wolfram.com/language/ref/Element.html (updated 2014).
CMS
Wolfram Language. 1999. "Element." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/Element.html.
APA
Wolfram Language. (1999). Element. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Element.html
BibTeX
@misc{reference.wolfram_2025_element, author="Wolfram Research", title="{Element}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/Element.html}", note=[Accessed: 05-October-2025]}
BibLaTeX
@online{reference.wolfram_2025_element, organization={Wolfram Research}, title={Element}, year={2014}, url={https://reference.wolfram.com/language/ref/Element.html}, note=[Accessed: 05-October-2025]}