FactorialMoment
FactorialMoment[data,r]
给出 data 的阶 r 阶乘矩 ![]() .
.
FactorialMoment[data,{r1,…,rm}]
给出 data 的阶 {r1,…,rm} 多元阶乘矩 ![]() .
.
FactorialMoment[dist,…]
给出了分布 dist 的阶乘矩.
代表阶 r 形式阶乘矩.
更多信息


- 阶乘矩使用 FactorialPower[x,r] 定义,由
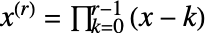 给出.
给出. - 对于标量阶 r 和作为数组的 data
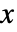 :
: -
![x in TemplateBox[{Vectors, paclet:ref/Vectors}, RefLink, BaseStyle -> {3ColumnTableMod}][n] x in TemplateBox[{Vectors, paclet:ref/Vectors}, RefLink, BaseStyle -> {3ColumnTableMod}][n]](Files/FactorialMoment.zh/6.png)
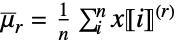
r  次阶乘幂之和 »
次阶乘幂之和 »![x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}] x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}]](Files/FactorialMoment.zh/9.png)
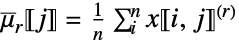
r  次阶乘幂列式之和 »
次阶乘幂列式之和 »![x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}] x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}]](Files/FactorialMoment.zh/12.png)
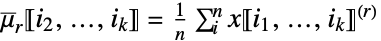
r  次阶乘幂列式之和 »
次阶乘幂列式之和 » - FactorialMoment[x,r] 等价于 ArrayReduce[FactorialMoment[#,r]&,x,1].
- 对于向量阶 {r1,…,rm} 和作为数组的 data
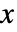 :
: -
![x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}] x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}]](Files/FactorialMoment.zh/16.png)
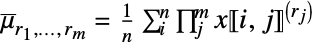
第 j 列中的 rj 次阶乘和 ![x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}] x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}]](Files/FactorialMoment.zh/18.png)
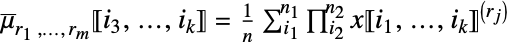
第 j 列中求和 rj 次阶乘幂 » - FactorialMoment[x,{r1,…,rm}] 等价于 ArrayReduce[FactorialMoment[#,{r1,…,rm}]&,x,{{1},{2}}].
- FactorialMoment 既能处理数值数据,也能处理符号数据.
- data 可以有以下其他形式和解释:
-
Association 值(忽略键值) » WeightedData 加权平均值,基于底层 EmpiricalDistribution » EventData 基于底层 SurvivalDistribution » TimeSeries, TemporalData, … 值的向量或数组(忽略时间戳) » Image,Image3D RGB 通道值或灰度强度值 » Audio 所有通道的振幅值 » - 对于分布 dist,第 r 次阶乘矩由 Expectation[x(r),xdist] 给出. »
- 对于多元分布 dist,第 {r1,…,rm}
 次阶乘矩由 Expectation[x1(r1)⋯ xm(rm),{x1,…,xm}dist] 给出. »
次阶乘矩由 Expectation[x1(r1)⋯ xm(rm),{x1,…,xm}dist] 给出. » - 对于随机过程 proc,可以计算出时间 t 的切片分布的阶乘矩函数 SliceDistribution[proc,t],因为
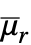 [t]=FactorialMoment[SliceDistribution[proc,t],r]. »
[t]=FactorialMoment[SliceDistribution[proc,t],r]. » - FactorialMoment[r] 可用于如 MomentConvert 和 MomentEvaluate 等函数. »
范例
打开所有单元关闭所有单元范围 (20)
基础用法 (5)
数组数据 (4)
对于矩阵而言,FactorialMoment 给出列向矩:
对于数组而言,FactorialMoment 给出第一层的列向矩:
数组的多元 FactorialMoment:
当输入是 Association 时,FactorialMoment 会作用于其值:
SparseArray 数据可以像稠密数组一样使用:
图像和音频数据 (2)
分布与过程矩 (5)
求 TemporalData 在某时刻 t=0.5 的阶乘矩:
形式矩 (4)
应用 (4)
属性和关系 (5)
阶乘矩 ![]() 与 FactorialPower 的期望等价:
与 FactorialPower 的期望等价:
第一阶乘矩与 Mean 等价:
FactorialMoment 可以由 Moment 通过 ![]() 计算:
计算:
MomentConvert 产生相同的结果:
Moment 可由 FactorialMoment 通过 ![]() 计算:
计算:
MomentConvert 产生相同的结果:
巧妙范例 (1)
估计 30、100 和 300 个样本的 FactorialMoment 的分布:
文本
Wolfram Research (2010),FactorialMoment,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FactorialMoment.html (更新于 2024 年).
CMS
Wolfram 语言. 2010. "FactorialMoment." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/FactorialMoment.html.
APA
Wolfram 语言. (2010). FactorialMoment. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FactorialMoment.html 年