FactorialPower
FactorialPower[x,n]
gives the factorial power ![]() .
.
FactorialPower[x,n,h]
gives the step-h factorial power ![]() .
.
Details

- Mathematical function, suitable for both symbolic and numeric manipulation.
- For integer n,
![TemplateBox[{x, n}, FactorialPower] TemplateBox[{x, n}, FactorialPower]](Files/FactorialPower.en/3.png) is given by
is given by 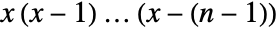 , and
, and ![TemplateBox[{x, n, h}, FactorialPower3] TemplateBox[{x, n, h}, FactorialPower3]](Files/FactorialPower.en/5.png) is given by
is given by 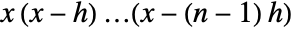 .
. ![TemplateBox[{x, n}, FactorialPower] TemplateBox[{x, n}, FactorialPower]](Files/FactorialPower.en/7.png) is given for any n by
is given for any n by ![TemplateBox[{{x, +, 1}}, Gamma]/TemplateBox[{{x, -, n, +, 1}}, Gamma] TemplateBox[{{x, +, 1}}, Gamma]/TemplateBox[{{x, -, n, +, 1}}, Gamma]](Files/FactorialPower.en/8.png) .
.![TemplateBox[{TemplateBox[{x, k}, FactorialPower], x}, DifferenceDelta2] TemplateBox[{TemplateBox[{x, k}, FactorialPower], x}, DifferenceDelta2]](Files/FactorialPower.en/9.png) is given by
is given by ![k TemplateBox[{x, {k, -, 1}}, FactorialPower] k TemplateBox[{x, {k, -, 1}}, FactorialPower]](Files/FactorialPower.en/10.png) and
and ![sum_xTemplateBox[{x, k}, FactorialPower] sum_xTemplateBox[{x, k}, FactorialPower]](Files/FactorialPower.en/11.png) is given by
is given by ![TemplateBox[{x, {k, +, 1}}, FactorialPower]/(k+1) TemplateBox[{x, {k, +, 1}}, FactorialPower]/(k+1)](Files/FactorialPower.en/12.png) .
.- FactorialPower[x,n] evaluates automatically only when x and n are numbers.
- FunctionExpand always converts FactorialPower to a polynomial or combination of gamma functions.
- FactorialPower can be used with Interval and CenteredInterval objects. »
Examples
open allclose allBasic Examples (7)
Find the "factorial square" of 10:
FactorialPower does not automatically expand out:
Use FunctionExpand to do the expansion:
Plot over a subset of the reals:
Plot over a subset of complexes:
Series expansion at the origin:
Series expansion at Infinity:
Scope (34)
Numerical Evaluation (7)
The precision of the output tracks the precision of the input:
Evaluate efficiently at high precision:
FactorialPower threads elementwise over lists:
Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:
Or compute average-case statistical intervals using Around:
Compute the elementwise values of an array:
Or compute the matrix FactorialPower function using MatrixFunction:
Specific Values (6)
Values of FactorialPower at fixed points:
Obtain the polynomial representation FactorialPower[x,n] for integer values of n:
With step ![]() , FactorialPower[x,n,h] gives the rising factorial:
, FactorialPower[x,n,h] gives the rising factorial:
This is equivalent to Pochhammer:
Expand FactorialPower[x,n] for a fixed value of x:
Do the same while adding integer values for the third argument:
Value with second argument zero:
Value with first argument 0 and positive second argument:
Find a value of x for which FactorialPower[x,1/7]=1.2:
Visualization (3)
Plot the FactorialPower function for various orders:
Plot FactorialPower as a function of its parameter ![]() :
:
Function Properties (10)
Real domain of the factorial power:
Function range of FactorialPower[x,n] for various fixed values of n:
![]() is neither nondecreasing nor nonincreasing:
is neither nondecreasing nor nonincreasing:
FactorialPower is neither non-negative nor non-positive:
![]() has potential singularities and discontinuities when
has potential singularities and discontinuities when ![]() is a negative integer:
is a negative integer:
![]() is neither convex nor concave:
is neither convex nor concave:
TraditionalForm formatting:
Differentiation (3)
Series Expansions (3)
Find the Taylor expansion using Series:
Plots of the first two approximations around ![]() :
:
Taylor expansion at a generic point:
FactorialPower can be applied to a power series:
Applications (4)
The number of length-r permutations of a length-n list of distinct elements is given by FactorialPower[n,r]:
The number of triples of distinct digits:
Approximate a function using Newton's forward difference formula [MathWorld]:
Properties & Relations (11)
FactorialPower is to Sum as Power is to Integrate:
FactorialPower satisfies ![]() :
:
This makes FactorialPower analogous to Power and its relationship to D:
FactorialPower can always be expressed as a ratio of gamma functions:
Compare with the expansion of ![]() :
:
FactorialPower[x,n] is equivalent to ![]() :
:
FactorialPower[x,x] is equivalent to x!:
Pochhammer can be expressed in terms of a single FactorialPower expression:
Verify the identity ![]() for integer
for integer ![]() :
:
This function is often called the rising factorial:
Verify an expansion of FactorialPower in terms of Pochhammer for the first few cases:
FactorialPower can be represented as a DifferenceRoot:
The generating function for FactorialPower:
The exponential generating function for FactorialPower:
Possible Issues (2)
Generically, Power is recovered as the limit as ![]() of FactorialPower:
of FactorialPower:
This may not be true, however, if ![]() is kept on the negative real axis:
is kept on the negative real axis:
The generic series expansion around the origin may not be defined at integer points:
Text
Wolfram Research (2008), FactorialPower, Wolfram Language function, https://reference.wolfram.com/language/ref/FactorialPower.html.
CMS
Wolfram Language. 2008. "FactorialPower." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FactorialPower.html.
APA
Wolfram Language. (2008). FactorialPower. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FactorialPower.html