FactorialPower
FactorialPower[x,n]
階乗ベキ ![]() を与える.
を与える.
FactorialPower[x,n,h]
![]() の階乗ベキをステップ h で与える.
の階乗ベキをステップ h で与える.
詳細

- 記号操作・数値操作の両方に適した数学関数である.
- 整数 n に対し,
![TemplateBox[{x, n}, FactorialPower] TemplateBox[{x, n}, FactorialPower]](Files/FactorialPower.ja/3.png) は
は 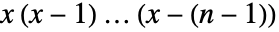 で与えられ,
で与えられ,![TemplateBox[{x, n, h}, FactorialPower3] TemplateBox[{x, n, h}, FactorialPower3]](Files/FactorialPower.ja/5.png) は
は 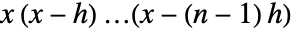 で与えられる.
で与えられる. ![TemplateBox[{x, n}, FactorialPower] TemplateBox[{x, n}, FactorialPower]](Files/FactorialPower.ja/7.png) は任意の n に対して
は任意の n に対して![TemplateBox[{{x, +, 1}}, Gamma]/TemplateBox[{{x, -, n, +, 1}}, Gamma] TemplateBox[{{x, +, 1}}, Gamma]/TemplateBox[{{x, -, n, +, 1}}, Gamma]](Files/FactorialPower.ja/8.png) で与えられる.
で与えられる.![TemplateBox[{TemplateBox[{x, k}, FactorialPower], x}, DifferenceDelta2] TemplateBox[{TemplateBox[{x, k}, FactorialPower], x}, DifferenceDelta2]](Files/FactorialPower.ja/9.png) は
は ![k TemplateBox[{x, {k, -, 1}}, FactorialPower] k TemplateBox[{x, {k, -, 1}}, FactorialPower]](Files/FactorialPower.ja/10.png) で与えられ,
で与えられ,![sum_xTemplateBox[{x, k}, FactorialPower] sum_xTemplateBox[{x, k}, FactorialPower]](Files/FactorialPower.ja/11.png) は
は ![TemplateBox[{x, {k, +, 1}}, FactorialPower]/(k+1) TemplateBox[{x, {k, +, 1}}, FactorialPower]/(k+1)](Files/FactorialPower.ja/12.png) で与えられる.
で与えられる.- FactorialPower[x,n]は x と n が数のときにのみ自動的に評価される.
- FunctionExpandは常にFactorialPowerを多項式かガンマ関数の組合せに変換する.
- FactorialPowerはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる. »
例題
すべて開くすべて閉じる例 (7)
スコープ (34)
数値評価 (7)
FactorialPowerは要素単位でリストに縫い込まれる:
IntervalオブジェクトとCenteredIntervalオブジェクトを使って最悪の場合に保証される区間を計算する:
Aroundを使って平均的な場合の統計区間を計算することもできる:
MatrixFunctionを使って行列のFactorialPower関数を計算することもできる:
特定の値 (6)
固定点におけるFactorialPowerの値:
n の整数値について多項式表現FactorialPower[x,n]を得る:
刻み幅が ![]() のとき,FactorialPower[x,n,h]は昇階乗ベキを与える:
のとき,FactorialPower[x,n,h]は昇階乗ベキを与える:
これはPochhammerに等しい:
x の固定値についてFactorialPower[x,n]を展開する:
FactorialPower[x,1/7]=1.2となるような x の値を求める:
可視化 (3)
関数の特性 (10)
級数展開 (3)
アプリケーション (4)
異なる要素の長さ n のリストの長さ r の順列の数は,FactorialPower[n,r]によって与えられる:
ニュートン(Newton)の前進差分公式[MathWorld]を使って関数を近似する:
特性と関係 (11)
FactorialPowerのSumに対する関係はPowerのIntegrateに対する関係に等しい:
FactorialPowerは ![]() を満足する:
を満足する:
これで,FactorialPowerはPowerに類似していることになり,Dとの関係が決まる:
FactorialPowerは常にガンマ関数の比で表すことができる:
FactorialPower[x,n]は ![]() に等しい:
に等しい:
FactorialPower[x,x]は x!と等価である:
Pochhammerは単一のFactorialPower式で表すことができる:
最初のいくつかのケースについて,PochhammerによるFactorialPowerの展開を検証する:
FactorialPowerはDifferenceRootとして表すことができる:
FactorialPowerの母関数:
FactorialPowerの指数母関数:
考えられる問題 (2)
一般に,PowerはFactorialPowerの ![]() のときの極限として復元される:
のときの極限として復元される:
しかし,![]() が負の実軸上にあればこれは真ではないかもしれない:
が負の実軸上にあればこれは真ではないかもしれない:
テキスト
Wolfram Research (2008), FactorialPower, Wolfram言語関数, https://reference.wolfram.com/language/ref/FactorialPower.html.
CMS
Wolfram Language. 2008. "FactorialPower." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FactorialPower.html.
APA
Wolfram Language. (2008). FactorialPower. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FactorialPower.html