FindFit
FindFit[data,expr,pars,vars]
求出参数 pars 的数值,使 expr 作为关于 vars 的函数给出对 data 最佳拟合.
FindFit[data,{expr,cons},pars,vars]
在带参量的约束条件 cons 下,求最佳拟合.
更多信息和选项




- data 可以采用形式 {{x1,y1,…,f1},{x2,y2,…,f2},…},其中坐标 x, y, … 的个数等于列表 vars 中变量的个数.
- data 也可以采用形式 {f1,f2,…},假定单坐标取值 1、2、….
- FindFit 返回一个替换 par1、par2、… 的列表.
- 当 pars 和 vars 都为数值时,则表达式 expr 必定产生一个数值.
- 表达式 expr 可以线性或非线性地依赖于 pari.
- 在线性情况下,FindFit 求出全局最优拟合.
- 在非线性情况下,FindFit 通常求出局部最优拟合.
- FindFit[data,expr,{{par1,p1},{par2,p2},…},vars] 开始搜索一个具有 {par1->p1,par2->p2,…} 的拟合.
- 在默认的情况下,FindFit 求出一个最小平方拟合.
- NormFunction->f 选项指定范式 f[residual] 应该被最小化.
- 约束条件 cons 可以包含方程、不等式或它们的逻辑组合.
- 可以给出以下选项:
-
AccuracyGoal Automatic 搜索的精确度 EvaluationMonitor None 当计算 expr 值时,运行的表达式 FitRegularization None 为模型 pars 的正则化 Gradient Automatic expr 的梯度分量列表 MaxIterations Automatic 使用的最大迭代次数 Method Automatic 所使用的方法 NormFunction Norm 最小化的范式 PrecisionGoal Automatic 搜索的精度 StepMonitor None 计算表达式时的步长 WorkingPrecision Automatic 内部计算采用的精度 - AccuracyGoal 和 PrecisionGoal 的默认设置是 WorkingPrecision/2.
- AccuracyGoal 和 PrecisionGoal 的设置指定返回参数值的位数和 NormFunction 的值.
- 当 NormFunction->f 且 FitRegularization->rfun,Fit 找到最小化 pars normf[{expr(pars,x1,y1,…)-f1,…}]+rfun[pars] 的 pars 值.
- NormFunction 的设置按以下形式给出:
-
f 应用于残差的函数 f {"HuberPenalty",α} 每个分量的 Huber 惩罚函数的和 {"DeadzoneLinearPenalty",α} 每个分量的死区线性惩罚函数之和 - FitRegularization 的设置可以是以下格式:
-
None 无正则化 rfun rfun[a] 的正则化 {"Tikhonov", λ} 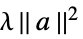 的正则化
的正则化{"LASSO",λ} 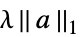 的正则化
的正则化{"Variation",λ} ![lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a]||^2 lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a]||^2](Files/FindFit.zh/3.png) 的正则化
的正则化{"TotalVariation",λ} ![lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a]||_1 lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a]||_1](Files/FindFit.zh/4.png) 的正则化
的正则化{"Curvature",λ} ![lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a,2]||^2 lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a,2]||^2](Files/FindFit.zh/5.png) 的正则化
的正则化{r1,r2,…} 带有来自 r1,… 和项的正则化 - FindFit 将继续计算,直到 AccuracyGoal 或 PrecisionGoal 指定的目标达到.
- Method 的通常设置包括 "ConjugateGradient"、"PrincipalAxis"、"LevenbergMarquardt"、"Newton" 和 "QuasiNewton",默认设置是 Automatic.
范例
打开所有单元关闭所有单元范围 (7)
简单指数拟合 (3)
约束条件和起始值 (2)
选项 (7)
应用 (7)
实验数据 (3)
微分方程 (2)
用 NDSolve 求解 PDE,获得空间网格:
属性和关系 (6)
FindFit 给出参数估计:
NonlinearModelFit 允许提取拟合的其他信息:
对于线性模型,Fit 等于 FindFit,并使用 LeastSquares:
用 Fit,设置基为 {1,x,x2}:
这等价于 FindFit,其模型函数的基是一个线性组合:
建立一个设计矩阵,用 LeastSquares 求出系数:
LinearModelFit 拟合线性模型,并提供额外的拟合结果:
FindFit 实际上使用 FindMinimum 最小化余差函数的范式:
默认情况下,FindFit 给出符合正态分布的结果:
LogitModelFit 假定二项分布响应:
对于 ProbitModelFit 也是如此:
GeneralizedLinearModelFit 允许二项式和其他分布结构.
FindFit 将 TimeSeries 的时间戳作为变量使用:
FindFit 对多路径 TemporalData 分别作用:
文本
Wolfram Research (2003),FindFit,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FindFit.html (更新于 2019 年).
CMS
Wolfram 语言. 2003. "FindFit." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2019. https://reference.wolfram.com/language/ref/FindFit.html.
APA
Wolfram 语言. (2003). FindFit. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FindFit.html 年