Fit

Fit[data,{f1,…,fn},{x,y,…}]

変数{x,y,…}の関数 f1,…,fnについての data のリストに対するフィット a1 f1+…+an fnを求める．

Fit[{m,v}]

計画行列 m についてを最小化するフィットベクトル a を求める．

Fit[…,"prop"]

どのフィット特性 prop を返すべきかを指定する．

詳細とオプション

  • Fitは，線形回帰あるいは最小二乗フィットとしても知られている．正則化では，LASSO回帰およびリッジ回帰としても知られている．
  • Fitは，一般に，多項式や指数関数を含む関数の組合せをデータにフィットする際に使用される．これは，データからモデルを得る最も簡単な方法の一つを提供する．
  • 最適フィットは，平方の和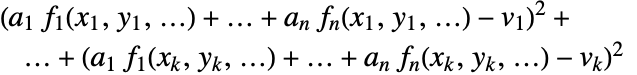を最小にする．
  • data は次の形式でよい．
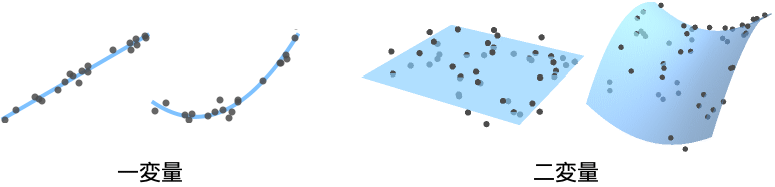
  • {v1,…,vn}{{1,v1},…,{n,vn}}と同等
    {{x1,v1},…,{xn,vn}}座標 xiにおける値 viを持った一変量データ
    {{x1,y1,v1},…}値 vi と座標{xi,yi}を持った二変量データ
    {{x1,y1,…,v1},…}座標{xi,yi,…}における値 viを持った多変量データ
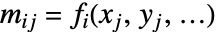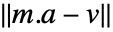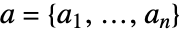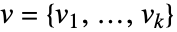  • 計画行列 m は座標位置で関数を評価して得られる要素 を持つ．行列表現では，最適フィットはノルムを最小化する．ただし，かつ である．
  • 関数 fi が依存するのは変数{x,y,…}だけでなければならない．
  • 可能なフィット特性"prop"には次がある．
  • "BasisFunctions"funs基底関数
    "BestFit"基底関数の最適フィット線形結合
    "BestFitParameters"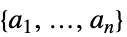最適フィットを与えるベクトル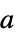
    "Coordinates"{{x1,y1,…},…}data 中の vars の座標
    "Data"dataデータ
    "DesignMatrix"m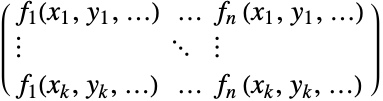
    "FitResiduals"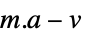座標におけるモデルとフィットの差
    "Function"Function[{x,y,…},a1 f1+…+an fn]最適フィット純関数
    "PredictedResponse"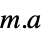data 座標についてフィットされた値
    "Response"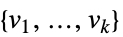入力 data からの応答ベクトル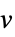
    {"prop1","prop2",…} いくつかのフィット特性
  • Fitは次のオプションを取る．
  • NormFunction Norm最小化する偏差の測定値
    FitRegularization Noneフィットパラメータ 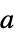についての正規化
    WorkingPrecision Automatic使用精度
  • NormFunction->normf かつFitRegularization->rfun のとき，Fitは normf[{a.f(x1,y1,…)-v1,…,a.f(xk,yk,…)-vk}] + rfun[a]を最小化する係数 a ベクトルを求める．
  • NormFunctionの設定は次の形式で与えることができる．
  • normf偏差に適用される関数 normf
    {"Penalty", pf}偏差の各成分に適用されたペナルティ関数 pf の和
    {"HuberPenalty",α}各成分についてのHuberペナルティ関数の和
    {"DeadzoneLinearPenalty",α}各成分についてのデッドゾーン線形ペナルティ関数の和
  • FitRegularizationの設定は次の形式で与えることができる．
  • None正規化は行わない
    rfunrfun[a]による正規化
    {"Tikhonov",λ}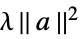による正規化
    {"LASSO",λ}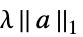による正規化
    {"Variation",λ}lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a]||^2による正規化
    {"TotalVariation",λ}lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a]||_1による正規化
    {"Curvature",λ}lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a,2]||^2による正規化
    {r1,r2,…}r1,…の項目の和による正規化
  • WorkingPrecision->Automaticのとき，Fitへの入力として与えられた厳密数は機械精度の近似数に変換される．

例題

すべて開くすべて閉じる

例  (2)

ここにあるデータがある：

このデータに最もよくフィットする線を求める：

このデータに最もよくフィットする二次関数を求める：

このデータを2本の曲線で示す：

計画行列と応答ベクトルが与えられたときの最適フィットパラメータを求める：

スコープ  (2)

ここに，厳密値で定義されたデータがある：

機械演算でこのデータを正弦関数の線形結合にフィットさせる：

24桁精度演算でデータをフィットする：

曲線でデータを示す：

ここに三次元データがある：

このデータに最もよくフィットする平面を求める：

データ点で平面を示す：

データに最もよくフィットする二次関数を求める：

この二次関数は実際にデータを補間する：

一般化と拡張  (1)

ここに値のリストがある：

二次関数にフィットする．座標は，与えられていなければ，値は1, 2, ...のペアとみなされる：

四次関数にフィットする：

曲線でデータを示す：

オプション  (6)

FitRegularization  (2)

Tikhonov正規化は最適フィットパラメータの大きさを制御する：

正規化がなければ，係数は極めて大きくなる：

これは，"L2"または"RidgeRegression"で参照することができる：

LASSO (least absolute shrinkage and selection operator) 正規化は，最も重要な基底関数を選択し，最適合パラメータの大きさをある程度制御する：

正規化なしでは係数はかなり大きい：

これは"L1"で参照することができる：

NormFunction  (3)

1ノルムを使って「最適」フィットを測定する：

最小二乗フィット（金）および最大ノルムフィット（緑）と比較する：

ノルム p をインタラクティブに操作する：

Huberのペナルティ関数を使って外れ値の影響と最小二乗のバランスを取る：

パラメータ をインタラクティブに操作する：

重み付き最小二乗フィットを計算する：

WorkingPrecision  (1)

24桁精度を使ってフィットを計算する：

厳密計算を使う：

アプリケーション  (6)

チェビシェフ(Chebyshev)基底を使ってデータへの高次多項式フィットを計算する：

正規化を使って が摂動する場合の の に対する数値解を安定させる：

LinearSolveによって求まった解には非常に大きい項がある：

正規化された解は非摂動問題の解の非常に近くにとどまる：

変動の正規化を使って入力信号に対する滑らかな近似を求める：

出力のターゲットは階段関数である：

によるたたみ込みによって，入力は出力から決定される：

正規化なしでは，予想された応答は信号に非常に近いが，計算された入力には大きな振動がある：

変動を正規化すると，はるかに滑らかな近似が求まる：

入力サイズの正規化も含まれることがある：

変動の正規化を使って破損信号を滑らかにする：

残差のノルムと変動のノルムの間のトレードオフをプロットする：

曲線が急激に曲がる場所近くの の値を選ぶ：

全変動の正規化を使ってジャンプがある破損信号を滑らかにする：

パラメータ で正規化する：

の値を小さくするとあまり滑らかではなくなるが，残差ノルムは小さくなる：

LASSO (L1)正規化を使って疎なフィット（基底追跡）を求める：

以下が信号である：

目標は，何千とあるGabor基底関数のいくつかを使って信号を近似することである：

のときのフィットは基底要素のたった41個を使って求めることができる：

誤差は極めて小さい：

基底の重要な要素が見付かったら，これらの要素の最小二乗フィットを求めることで誤差を小さくすることができる：

より小さな値の でのフィットもほぼ同じ要素を使って求めることができる：

誤差はさらに小さい：

特性と関係  (5)

Fitは最適フィットの関数を与える：

LinearModelFitはフィットに関する追加的な情報の抽出を許す：

フィットされた関数を抽出する：

追加的な結果と診断を抽出する：

ここにデータがある：

これは，直線a+b xの誤差の平方和である：

最小値を記号的に求める：

以下はFitで与えられる係数である：

厳密係数はWorkingPrecision->Infinityを使うと求まるかもしれない：

これは，二次方程式a+b x+c x^2の誤差の平方和である：

最小値を記号的に求める：

これらはFitで与えられる係数である：

多項式のフィットが十分高い次数で行われるとき，Fitは補間多項式を返す：

結果はInterpolatingPolynomialで返されるものと矛盾しない：

Fit は，TimeSeriesのタイムスタンプを変数として使う：

タイムスタンプを再スケールし，フィットし直す：

値についてのフィットを求める：

Fitは，複数の経路があるTemporalDataについては，経路ごとに作用する：

考えられる問題  (2)

ここに，ガウス分布のランダムな摂動からのデータがある：

これは多項式の標準基底を与える関数である：

次数が高くなる多項式について計算したフィットを示す：

問題はベキが高くなると係数が非常に小さくなる点である：

基底をスケールされシフトされた値で与えると問題の助けになる：

圧縮されたセンシングデータから疎な信号を再構築する：

長さ のデータだけが送信されるように，信号に の 行列を掛けてセンシングデータを圧縮する． が十分に大きければ，独立かつ一様に分布した正規項を持つランダム行列は，制約された等尺性を満足し，もとの信号を非常に高い確率で回復することができる：

送信するサンプルは信号に行列 を掛けて構築される：

再構築は， の可能なすべての解について，を最小にすることで行われる：

最小化が線形最適化で解かれたとしても，すべての制約条件が等式制約なので，その過程は比較的遅い．基底追跡（L1型正則化 ）を使うと，はるかに速く解を求めることができる：

次は基底要素を与える．最適解を求めたければ，これらの成分に対応する線形方程式を解くとよい：

Wolfram Research (1988), Fit, Wolfram言語関数， https://reference.wolfram.com/language/ref/Fit.html （2019年に更新）.

テキスト

Wolfram Research (1988), Fit, Wolfram言語関数， https://reference.wolfram.com/language/ref/Fit.html （2019年に更新）.

CMS

Wolfram Language. 1988. "Fit." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/Fit.html.

APA

Wolfram Language. (1988). Fit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Fit.html

BibTeX

@misc{reference.wolfram_2024_fit, author="Wolfram Research", title="{Fit}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Fit.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_fit, organization={Wolfram Research}, title={Fit}, year={2019}, url={https://reference.wolfram.com/language/ref/Fit.html}, note=[Accessed: 17-November-2024 ]}