Fit

Fit[data,{f1,…,fn},{x,y,…}]

求变量{x,y,…} 的函数 f1,…,fn 的 data 列表拟合 a1 f1+…+an fn.

Fit[{m,v}]

求最小化设计矩阵 m 的 的拟合向量 a.

Fit[…,"prop"]

指定应返回哪些拟合属性 prop.

更多信息和选项

  • Fit 也被称为线性回归或最小二乘拟合. 如果再加上正则化，也可被称为 LASSO 和岭回归.
  • Fit 通常用于将函数组合拟合到数据，包括多项式和指数. 它提供了从数据中获取模型的最简单方法之一.
  • 最佳拟合最小化平方和 .
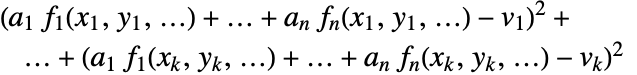  • data 可以是以下格式：
  • {v1,…,vn}等同于 {{1,v1},…,{n,vn}}
    {{x1,v1},…,{xn,vn}}在坐标 xi 具有值 vi 的单变量数据
    {{x1,y1,v1},…}在坐标 {xi,yi} 具有值 vi 的双变量数据
    {{x1,y1,…,v1},…}在坐标 {xi,yi,…} 具有值 vi 的多变量数据
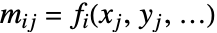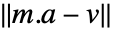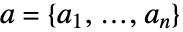  • 设计矩阵 m 具有在坐标 计算函数的元素. 在矩阵记法中，最佳拟合最小化范数 ，其中， 且 .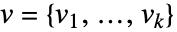
  • 函数 fi 应该只依赖于变量 {x,y,…}.
  • 可能的拟合属性 "prop" 包括：
  • "BasisFunctions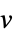vfuns基本函数
    "BestFit"基本函数的最佳拟合线性组合
    "BestFitParameters"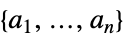给出最佳拟合的向量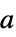
    "Coordinates"{{x1,y1,…},…}data 中 vars 的坐标
    "Data"data数据
    "DesignMatrix"m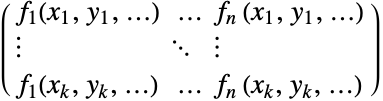
    "FitResiduals"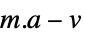坐标中模型和拟合之间的差
    "Function"Function[{x,y,…},a1 f1+…+an fn]最佳拟合纯函数
    "PredictedResponse"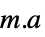data 坐标的拟合值
    "Response"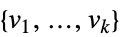来自输入 data 的响应向量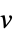
    {"prop1","prop2",…} 多个拟合属性
  • Fit 接受以下选项：
  • NormFunction Norm衡量最小化偏差
    FitRegularization None拟合参数 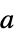的正则化
    WorkingPrecision Automatic使用的精度
  • 当 NormFunction->normf 且 FitRegularization->rfun，Fit 找到最小化 normf[{a.f(x1,y1,…)-v1,…,a.f(xk,yk,…)-vk}] + rfun[a] 的系数向量 a.
  • NormFunction 的设置可以是以下格式：
  • normf应用于偏差的函数 normf
    {"Penalty", pf}应用于偏差的每个分量的惩罚函数 pf 之和
    {"HuberPenalty",α}每个分量的 Huber 惩罚函数之和
    {"DeadzoneLinearPenalty",α}每个分量的死区线性惩罚函数之和
  • FitRegularization 的设置可以是以下格式：
  • None无正则化
    rfun用 rfun[a] 正则化
    {"Tikhonov",λ}用 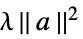正则化
    {"LASSO",λ}用 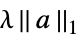正则化
    {"Variation",λ}用 lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a]||^2 正则化
    {"TotalVariation",λ}用 lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a]||_1 正则化
    {"Curvature",λ} lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a,2]||^2 正则化
    {r1,r2,…}用来自于 r1,… 项之和正则化
  • 当 WorkingPrecision->Automatic， 作为 Fit 输入的精确数字被转换成有机器精度的近似数字.

范例

打开所有单元关闭所有单元

基本范例  (2)

这里有一些数据：

求对数据进行最佳拟合的线：

求数据的最小二乘拟合：

用 2 条曲线显示数据：

求给出设计矩阵和响应向量的最佳拟合参数：

范围  (2)

以下是一些用精确值定义的数据：

使用机器算术将数据拟合为正弦函数的线性组合：

使用 24 位精度算术拟合数据：

用曲线显示数据：

以下是三维中的一些数据：

找到可最佳拟合数据的平面：

显示带有数据点的平面：

找到可最佳拟合数据的二次方：

二次方实际上是对数据进行插值：

推广和延伸  (1)

这是一个值的列表：

对二次拟合. 当坐标没有给出时，假定植为成对的1，2，…：

二次拟合：

用曲线显示数据：

选项  (6)

FitRegularization  (2)

Tikhonov 正则化控制最佳拟合参数的大小：

没有正则化，系数相当大：

这也可以用 "L2" 或 "RidgerRegression" 指代：

LASSO （最小绝对收缩和选择算子）正则化选择最重要的基函数，并对最佳拟合参数的大小进行一些控制：

没有正则化，系数是相当大的：

这也可以被 "L1" 引用：

NormFunction  (3)

使用 1-范数度量“最佳”拟合:

与最小二乘（金色）和最大范数（绿色）拟合比较：

交互式操作范数 p：

使用 Huber 惩罚函数来平衡具有最小二乘的异常值的影响：

交互式操作参数 ：

计算加权最小二乘拟合：

WorkingPrecision  (1)

使用 24 位精度计算拟合：

使用精确计算：

应用  (6)

使用 Chebyshev 基础计算适合数据的高次多项式：

使用正则化将数值解 稳定到 ，其中， 被扰动：

LinearSolve 找到的解有很大的项：

正则化的解更接近于未扰动问题的解：

使用变正则化求输入信号的平滑近似：

输出目标是阶跃函数：

输入由输出通过与 卷积决定：

没有正则化，谓词响应非常接近地匹配信号，但计算的输入有很多振荡：

通过变换的正则化，可以找到更平滑的近似值：

也可以包括输入大小的正则化：

使用变化正则化平滑损坏的信号：

绘制残差范数与变化范数之间的权衡：

在曲线急剧弯曲的位置附近选择 的值：

使用总变差正则化来平滑带有跳跃的损坏信号：

参数 的正则化：

较小的 值给出较少的平滑，但残差范数较小：

使用 LASSO (L1) 正则化来找到稀疏拟合（基追踪）：

信号：

目标是用几千个 Gabor 基函数中的少数几个来近似信号：

当 ，只需要 41 个基元素就可以找到拟合：

误差相当小：

一旦找到基础的重要元素，就可以通过找到最小二乘拟合这些这些元素来减少误差：

当更小的值 ，使用更多的基本元素找到拟合：

误差更小：

属性和关系  (5)

Fit 给出最佳拟合函数：

LinearModelFit 允许提取拟合的其他信息：

从拟合函数中提取信息：

提取其他结果和诊断：

这是一些数据：

这是直线 a+b x 的二次误差的和：

求符号最小值：

这是 Fit 给出的系数：

精确系数可以通过使用 WorkingPrecision->Infinity 找到：

这是二次表达式 a+b x+c x^2 的二次误差的和：

求符号最小值：

这是 Fit 给出的系数：

当一个多项式拟合执行到足够的次数，Fit 返回插值多项式：

结果与 InterpolatingPolynomial 给出的一致：

Fit 以变量的形式使用 TimeSeries 的时间戳：

缩放时间戳并且再次拟合：

求数值的拟合：

Fit 按路径作用于多条路径的 TemporalData:

可能存在的问题  (2)

这是一些高斯随机波动产生的数据：

这个函数给出了多项式的标准基：

显示连续高阶多项式的拟合计算：

问题时对高阶幂而言，系数非常小：

给出根据比例和位移值的基，有助于解决这个问题：

从压缩传感数据重建稀疏信号：

压缩感知包括将信号乘以 矩阵，其中 ，因此只需传输长度为 的数据. 如果 足够大，具有独立相同分布的正态条目的随机矩阵将满足受限制的等距属性，并且可以非常高的概率恢复原始信号：

要发送的样本是通过将信号与矩阵 相乘来构造的：

对于 的所有可能解决方案，可以通过最小化 进行重建：

即使最小化是通过线性优化解决的，但它相对较慢，因为所有约束都是等式约束. 使用基础追踪（L1 正则化）可以更快地找到解决方案：

这给出了基本要素. 要找到最佳解，求出与这些分量对应的线性方程：

Wolfram Research (1988)，Fit，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Fit.html （更新于 2019 年）.

文本

Wolfram Research (1988)，Fit，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Fit.html （更新于 2019 年）.

CMS

Wolfram 语言. 1988. "Fit." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2019. https://reference.wolfram.com/language/ref/Fit.html.

APA

Wolfram 语言. (1988). Fit. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Fit.html 年

BibTeX

@misc{reference.wolfram_2024_fit, author="Wolfram Research", title="{Fit}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Fit.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_fit, organization={Wolfram Research}, title={Fit}, year={2019}, url={https://reference.wolfram.com/language/ref/Fit.html}, note=[Accessed: 17-November-2024 ]}