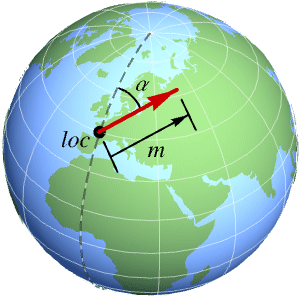
GeoVector

GeoVector[loc{m,α}]

represents a horizontal two-dimensional vector of magnitude m and bearing α at geo location loc.

GeoVector[loc{m,α,w}]

represents a three-dimensional vector of horizontal modulus m, bearing α and vertical component w at geo location loc.

GeoVector[{loc1,loc2,…}{vec1,vec2,…}]

represents a collection of vectors veci at respective geo locations loci.

GeoVector[{loc1vec1,loc2vec2,…}]

represents the same collection of vectors.

GeoVector[vec]

represents a geo vector whose associated location has been implicitly specified.

Details

  • GeoVector[…] can represent any vectorial magnitude on the surface of the Earth or any other celestial globe, like wind speed, magnetic field, scalar gradient, etc.
  • GeoVector describes vector data using an orthonormal frame tangent to the reference ellipsoid at the given location.
  • In GeoVector[loc{m,α}], the vector modulus m can be given as a numeric expression or numeric Quantity object with any units. The bearing α can be given as a number of degrees or a Quantity angle, measured clockwise from north. The vertical component is assumed to be zero.
  • In GeoVector[loc{m,α,w}], the horizontal modulus m and the vertical component w can be quantities, but their units must be compatible.
  • In GeoVector[locvec], the location loc can be given as a {lat,lon} pair in degrees, a geo Entity object or any geo location object with head GeoPosition or similar.
  • GeoVector[GeoVectorENU[…]] converts a vector in GeoVectorENU form to GeoVector form, and similarly for GeoVectorXYZ and GeoGridVector objects.
  • GeoGraphics[GeoVector[locvec]] takes loc into account for geo range estimation, but does not display a vector. Use GeoGraphics[GeoMarker[GeoVector[locvec],vmarker]] to display a vector at the given location, styled as specified by the vector marker vmarker.
  • GeoVector[…][prop] gives the specified property of a geo vector.
  • Possible properties include:
  		• "Count"number of vectors in the GeoVector object
    		"Data"first argument of the GeoVector object
    		"Depth"vector depth: 0 for a single vector, 1 for a list of them, …
    		"Location"location data of the GeoVector object
    		"LocationDimension"number of coordinates for each position
    		"LocationPackingType"Integer or Real if positions are packed; None otherwise
    		"Vector"vector data of the GeoVector object
    		"VectorDimension"number of components for each vector
    		"VectorPackingType"Integer or Real if vectors are packed; None otherwise

Examples

open allclose all

Basic Examples  (3)

Take current wind data near your location:

Place a dart with such direction in a local map of your area:

Show the direction in a world map with a different geo projection, using a smaller dart:

Get data about the Earth's magnetic field vector at Anchorage:

The horizontal component, declination and negative of the down component form a GeoVector object:

Transform that geo vector to its Cartesian form along the east-north-up axes:

Transform back to cylindrical form:

Draw arrows at random locations over the world, always pointing in the north direction:

Use GeoVectorPlot for a smoother representation:

Scope  (8)

Data Specification  (4)

Specify the location of a geo vector as a {lat,lon} pair in degrees:

Construct a horizontal velocity vector with 60 degrees bearing at Chicago:

Rewrite the location as a geo position object with any head:

Anything that can be interpreted by GeoPosition can be used as a location:

Work with horizontal 2D vectors with a non-negative modulus of any unit dimension:

Bearings can be given as a number of degrees or as a Quantity angle:

Geo Vector Arrays  (3)

Specify wind data simultaneously for several locations:

The same input can also be expressed as:

Represent those wind directions in a map:

Generate a million random Cartesian vectors at respective random locations:

GeoVector can process them efficiently:

Transform back to their Cartesian form:

Check that the difference is just numerical error:

Take the locations of the capital cities of the UN countries:

Construct random vectors at those locations:

Convert to local Cartesian form:

Convert back to polar form:

Data Extraction  (1)

A horizontal velocity vector with 60 degrees bearing at Chicago:

Extract the location of the geo vector:

Extract the vector data from the geo vector:

Extract the locvec rule:

Extract all properties:

Applications  (1)

Get vector field data for 100 random locations over Canada:

They roughly point north, but there is some variability:

Represent the horizontal part of those vectors in a cylindrical projection, for which the y axis points toward true north:

Properties & Relations  (4)

The same vector data at different locations represents different 3D vectors:

Identical vertical vectors at antipodal locations are opposite each other as 3D vectors:

This is an acceleration vector at the location of the Eiffel Tower:

Convert into a vector in the Mercator projection:

Transform back to GeoVector form:

Interactive Examples  (2)

Compare a geo vector and a geodesic starting from the same location with the same azimuth:

Draw the north and east directions at a chosen location, and a vector at that same location:

Wolfram Research (2019), GeoVector, Wolfram Language function, https://reference.wolfram.com/language/ref/GeoVector.html.

Text

Wolfram Research (2019), GeoVector, Wolfram Language function, https://reference.wolfram.com/language/ref/GeoVector.html.

CMS

Wolfram Language. 2019. "GeoVector." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GeoVector.html.

APA

Wolfram Language. (2019). GeoVector. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GeoVector.html

BibTeX

@misc{reference.wolfram_2024_geovector, author="Wolfram Research", title="{GeoVector}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/GeoVector.html}", note=[Accessed: 30-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_geovector, organization={Wolfram Research}, title={GeoVector}, year={2019}, url={https://reference.wolfram.com/language/ref/GeoVector.html}, note=[Accessed: 30-December-2024 ]}