GeometricTransformation

GeometricTransformation[g,tfun]

変換関数 tfun をプリミティブ g に対応する幾何学オブジェクトに適用した結果を表す．

GeometricTransformation[g,m]

実質的にすべての点 r を m.r で置換することで，g 中の幾何学オブジェクトを変換する．

GeometricTransformation[g,{m,v}]

実質的にすべての点 r を m.r+v で置換する．

GeometricTransformation[g,{t1,t2,…}]

一群の変換で変換された g の複数のコピーを表す．

詳細とオプション

  • GeometricTransformation[g,…]は評価では変化しないが，g がどのように描画されるかには影響を与える．
  • GeometricTransformationは二次元および三次元のグラフィックスプリミティブおよびグラフィックス指示子のリストに使うことができる．
  • GeometricTransformation[g,{m,v}]は実質的に g にアフィン変換を適用する．
  • GeometricTransformation[g,{{mxx,myx},{mxy,myy}}]は，単位ベクトルと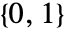をそれぞれ{mxx,mxy}と{myx,myy}に変換する．
  • 異なる spec について，GeometricTransformation[g,{m,spec}]は，g の境界ボックス上の次の特別な点を固定したままにする．
  • Center中央
    Left左辺の中央
    Right右辺の中央
    Top上辺の中央
    Bottom下辺の中央
    Front前面の中央
    Back裏面の中央
    {Left,Top}等角
  • スケールされた座標Scaled[{x,y}]で指定されたオブジェクトについて，GeometricTransformationは実質的に対応する通常の座標に変換を適用する．
  • Normal[expr]は，可能であれば，すべてのGeometricTransformation[gi,…]構文を，座標が明示的に変換された giのバージョンに置き換える．
  • 次のオプションを与えることができる．
  • ContentSelectableAutomaticコンテンツの選択を許容するかどうか
  • 行列 m1および m2について，GeometricTransformation[GeometricTransformation[g,m1],m2]はGeometricTransformation[g,m2.m1]に等しい．

例題

すべて開くすべて閉じる

例  (3)

2Dオブジェクトを変換する：

3Dオブジェクトを変換する：

同じオブジェクトに複数の変換を適用することができる：

スコープ  (5)

2Dの形に適用した変換：

3Dの形に適用した変換：

スケールされた座標のオブジェクト：

円の最も右寄りの点を固定したままにしておく：

ネストした変換を作成する：

特性と関係  (2)

{m,v}を第2引数として使うことはAffineTransform[{m,v}]を使うことに等しい：

Normalは可能な場合は明示的に変換を行う：

おもしろい例題  (1)

空間曲線に沿って直方体を回転させ移動させる：

Wolfram Research (2007), GeometricTransformation, Wolfram言語関数， https://reference.wolfram.com/language/ref/GeometricTransformation.html （2010年に更新）.

テキスト

Wolfram Research (2007), GeometricTransformation, Wolfram言語関数， https://reference.wolfram.com/language/ref/GeometricTransformation.html （2010年に更新）.

CMS

Wolfram Language. 2007. "GeometricTransformation." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2010. https://reference.wolfram.com/language/ref/GeometricTransformation.html.

APA

Wolfram Language. (2007). GeometricTransformation. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GeometricTransformation.html

BibTeX

@misc{reference.wolfram_2024_geometrictransformation, author="Wolfram Research", title="{GeometricTransformation}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/GeometricTransformation.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_geometrictransformation, organization={Wolfram Research}, title={GeometricTransformation}, year={2010}, url={https://reference.wolfram.com/language/ref/GeometricTransformation.html}, note=[Accessed: 21-November-2024 ]}