GeometricTransformation[g,tfun]
表示应用变换函数 tfun 到与图形基元 g 相对应的几何对象上.
通过把点 r 替换为 m.r,变换几何对象 g.
GeometricTransformation[g,{m,v}]
把每个点 r 替换为 m.r+v.
GeometricTransformation[g,{t1,t2,…}]
表示经过一组变换的 g 的多个版本.


GeometricTransformation
GeometricTransformation[g,tfun]
表示应用变换函数 tfun 到与图形基元 g 相对应的几何对象上.
通过把点 r 替换为 m.r,变换几何对象 g.
GeometricTransformation[g,{m,v}]
把每个点 r 替换为 m.r+v.
GeometricTransformation[g,{t1,t2,…}]
表示经过一组变换的 g 的多个版本.
更多信息和选项

- GeometricTransformation[g,…] 在计算下保持不变,但是影响 g 的绘制.
- GeometricTransformation 应用于二维和三维的图形基元和指令.
- GeometricTransformation[g,{m,v}] 有效地应用仿射转换到 g.
- GeometricTransformation[g,{{mxx,myx},{mxy,myy}}] 分别转换相应于{mxx,mxy} 和 {myx,myy} 的单位向量
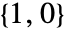 和
和 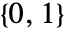 .
. - 对于不同的 spec,GeometricTransformation[g,{m,spec}] 留下以下固定的在 g 的边缘的特殊点:
-
Center 中间 Left 左边的中点 Right 右边的中点 Top 顶部的中点 Bottom 底部的中点 Front 前面的中点 Back 后面的中点 {Left,Top}等等 位于角上 - 对由标有刻度的指定坐标的对象 Scaled[{x,y}],GeometricTransformation 实际上应用它的转换到对应 的普通坐标.
- Normal[expr] 尽可能的替换所有由 gi 构建的 GeometricTransformation[gi,…],其中坐标已经变换.
- 以下选项被给出:
-
ContentSelectable Automatic 是否允许选择内容 - 对于矩阵 m1和 m2,GeometricTransformation[GeometricTransformation[g,m1],m2] 等价于 GeometricTransformation[g,m2.m1].
范例
打开所有单元 关闭所有单元属性和关系 (2)
相关的工作流程
- 旋转、平移和缩放三维图形
文本
Wolfram Research (2007),GeometricTransformation,Wolfram 语言函数,https://reference.wolfram.com/language/ref/GeometricTransformation.html (更新于 2010 年).
CMS
Wolfram 语言. 2007. "GeometricTransformation." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2010. https://reference.wolfram.com/language/ref/GeometricTransformation.html.
APA
Wolfram 语言. (2007). GeometricTransformation. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/GeometricTransformation.html 年
BibTeX
@misc{reference.wolfram_2025_geometrictransformation, author="Wolfram Research", title="{GeometricTransformation}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/GeometricTransformation.html}", note=[Accessed: 02-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_geometrictransformation, organization={Wolfram Research}, title={GeometricTransformation}, year={2010}, url={https://reference.wolfram.com/language/ref/GeometricTransformation.html}, note=[Accessed: 02-March-2026]}