WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

HermitianMatrix[hmat]

エルミート(Hermite)行列 hmat を構造化配列に変換する．

詳細とオプション
Details and Options Details and Options
例題  
例  
スコープ  
オプション  
TargetStructure  
アプリケーション  
特性と関係  
関連項目
関連するガイド
履歴
引用書式

HermitianMatrix

HermitianMatrix[hmat]

エルミート(Hermite)行列 hmat を構造化配列に変換する．

詳細とオプション

  • エルミート行列は，構造化配列として表されている場合は，便利な指定が利用できる．
  • エルミート行列の場合，アプリケーションで発生する固有値問題を非常に低コストで解くことができる．
  • エルミート行列 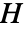は H〚i,j〛=TemplateBox[{{H, 〚, {j, ,, i}, 〛}}, Conjugate]を満足する．
  • 要素 hijは数値でなければならない．
  • エルミート行列の逆行列および一般にエルミート行列の任意の行列関数はエルミート行列である．
  • HermitianMatrix sa の次の特性"prop"には sa["prop"]でアクセスすることができる．
  • "Matrix"完全配列として表されるエルミート行列
    "Properties"サポートされる特性のリスト
    "Structure"構造化配列の型
    "StructuredData"構造化配列によって保存されている内部データ
    "StructuredAlgorithms"構造化配列についての特別なメソッドを持つ関数のリスト
    "Summary"Datasetとして表された情報の要約
  • Normal[HermitianMatrix[…]]はエルミート行列を通常の行列として与える．
  • HermitianMatrix[…,TargetStructure->struct]はエルミート行列を struct で指定された形式で与える．次は，使用可能な設定である．
  • Automatic返す表現を自動的に選択する
    "Dense"行列を密な行列として表す
    "Structured"行列を構造化配列として表す
  • HermitianMatrix[…,TargetStructureAutomatic]はHermitianMatrix[…,TargetStructure"Structured"]に等しい．

例題

すべて開く すべて閉じる

例  (1)

エルミート行列を構築する：

Wolfram Language code: hm = HermitianMatrix[{{1, 1 + I, 2I}, {1 - I, 5, -3}, {-2I, -3, 0}}]

要素を表示する：

Wolfram Language code: MatrixForm[hm]

NormalはHermitianMatrixを通常の表現に変換することができる：

Wolfram Language code: Normal[hm]

スコープ  (4)

エルミート行列をその上三角の成分から構築する：

Wolfram Language code: HermitianMatrix[{{1, 1 + I, 2I}, {5, -3}, {0}}]

要素を表示する：

Wolfram Language code: MatrixForm[%]

この行列はその下三角成分からも構築できる：

Wolfram Language code: HermitianMatrix[{{1}, {1 - I, 5}, {-2I, -3, 0}}]

ヒルベルト行列はエルミート行列である：

Wolfram Language code: hm = HermitianMatrix[HilbertMatrix[4]]

複素反射行列は，エルミート行列でありユニタリ行列でもある：

Wolfram Language code: rm = ReflectionMatrix[{I, -1, -I}]
Wolfram Language code: {HermitianMatrix[rm], UnitaryMatrix[rm]}

HermitianMatrixオブジェクトは行列についての情報を与える特性を含む：

Wolfram Language code: hm = HermitianMatrix[(⁠| | | | | | ------- | ------- | ------- | ------- | | 1 | 1 + 2 I | 1 + 3 I | 1 + 4 I | | 1 - 2 I | 2 | 2 + 3 I | 2 + 4 I | | 1 - 3 I | 2 - 3 I | 3 | 3 + 4 I | | 1 - 4 I | 2 - 4 I | 3 - 4 I | 4 |⁠)]
Wolfram Language code: hm["Properties"]


"Summary"特性は行列についての情報の簡単な要約を与える：

Wolfram Language code: hm["Summary"]

"StructuredAlgorithms"特性は構造化アルゴリズムを持つ関数をリストにする：

Wolfram Language code: hm["StructuredAlgorithms"]

オプション  (1)

TargetStructure  (1)

エルミート行列を密な行列として返す：

Wolfram Language code: HermitianMatrix[(⁠| | | | | ----- | ----- | --- | | 1 | 1 + I | 2 I | | 1 - I | 5 | -3 | | -2 I | -3 | 0 |⁠), TargetStructure -> "Dense"]

エルミート行列を構造化配列として返す：

Wolfram Language code: HermitianMatrix[(⁠| | | | | ----- | ----- | --- | | 1 | 1 + I | 2 I | | 1 - I | 5 | -3 | | -2 I | -3 | 0 |⁠), TargetStructure -> "Structured"]

アプリケーション  (3)

GaussianUnitaryMatrixDistributionから導かれた行列はエルミート行列である：

Wolfram Language code: HermitianMatrix[RandomVariate[GaussianUnitaryMatrixDistribution[9]]]

GaussianSymplecticMatrixDistributionから導かれた行列はエルミート行列である：

Wolfram Language code: HermitianMatrix[RandomVariate[GaussianSymplecticMatrixDistribution[9]]]

パウリ(Pauli)行列はエルミート行列である：

Wolfram Language code: PauliMatrix[Range[3], TargetStructure -> "Hermitian"]

正定値エルミート行列 は で内積を定義する：

Wolfram Language code: g = HermitianMatrix[{{7, 2 + I, 3I}, {2 - I, 6, -2}, {-3I, -2, 5}}]
Wolfram Language code: ip[u_, v_] := Conjugate[u].g.v

が正定値行列であることを確かめる：

Wolfram Language code: PositiveDefiniteMatrixQ[g]

TemplateBox[{}, Complexes]^nの標準基底を直交化して正規直交基底を求める：

Wolfram Language code: {Subscript[e, 1], Subscript[e, 2], Subscript[e, 3]} = Orthogonalize[IdentityMatrix[3], ip]

この基底が内積について正規直交であることを確認する：

Wolfram Language code: Table[ip[Subscript[e, i], Subscript[e, j]], {i, 3}, {j, 3}]//Simplify

特性と関係  (4)

エルミート行列の共役転置はもとの行列と等価である：

Wolfram Language code: hm = HermitianMatrix[(⁠| | | | | ---- | - | --- | | 1 | 0 | 2 I | | 0 | 2 | 0 | | -2 I | 0 | -1 |⁠)]
Wolfram Language code: ConjugateTranspose[hm] === hm

実数対称行列はエルミート行列でもある：

Wolfram Language code: hm = HermitianMatrix[(⁠| | | | | ----- | ----- | ----- | | 1 | (1/2) | (1/3) | | (1/2) | (1/3) | (1/4) | | (1/3) | (1/4) | (1/5) |⁠)]
Wolfram Language code: {HermitianMatrixQ[hm], SymmetricMatrixQ[hm] && MatrixQ[hm, RealValuedNumberQ]}

エルミート行列は，SymmetrizedArrayあるいはHermitianMatrixを使って表すことができる：

Wolfram Language code: array = SymmetrizedArray[{{1, 3} -> I, {2, 2} -> 2}, {3, 3}, Hermitian[All]]
Wolfram Language code: matrix = HermitianMatrix[{{0, 0, I}, {0, 2, 0}, {-I, 0, 0}}]

2つの表現は等価であるが，異なるアルゴリズムをサポートする：

Wolfram Language code: array == matrix

SymmetrizedArrayは，D，Flatten，Inner，Outerのようなテンソル操作をサポートする：

Wolfram Language code: array["StructuredAlgorithms"]

HermitianMatrixは，KroneckerProductのような行列特有の操作をサポートする：

Wolfram Language code: matrix["StructuredAlgorithms"]

実際のエルミート行列はSymmetricMatrixを使って表すこともできる：

Wolfram Language code: SymmetricMatrix[HermitianMatrix[(| | | | - | - | | 1 | 2 | | 2 | 3 |)]]

これは，複素エルミート行列については真ではない：

Wolfram Language code: SymmetricMatrix[HermitianMatrix[(| | | | ----- | ----- | | 1 | 2 + I | | 2 - I | 3 |)]]
Wolfram Research (2024), HermitianMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/HermitianMatrix.html.

テキスト

Wolfram Research (2024), HermitianMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/HermitianMatrix.html.

CMS

Wolfram Language. 2024. "HermitianMatrix." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/HermitianMatrix.html.

APA

Wolfram Language. (2024). HermitianMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HermitianMatrix.html

BibTeX

@misc{reference.wolfram_2026_hermitianmatrix, author="Wolfram Research", title="{HermitianMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/HermitianMatrix.html}", note=[Accessed: 02-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_hermitianmatrix, organization={Wolfram Research}, title={HermitianMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/HermitianMatrix.html}, note=[Accessed: 02-November-2026]}