WOLFRAM

Wolfram言語 ＆ システム ドキュメントセンター
Wolfram言語ホームページ »

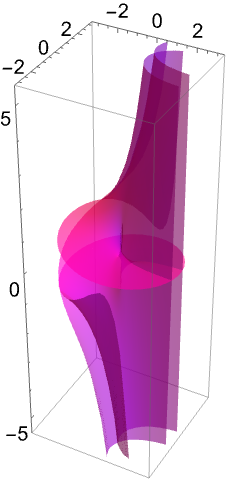
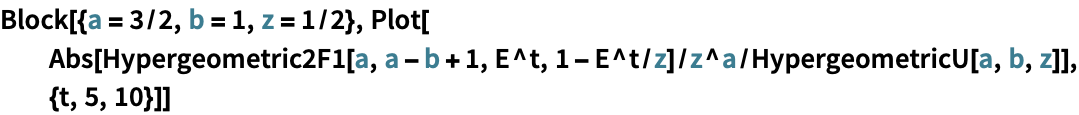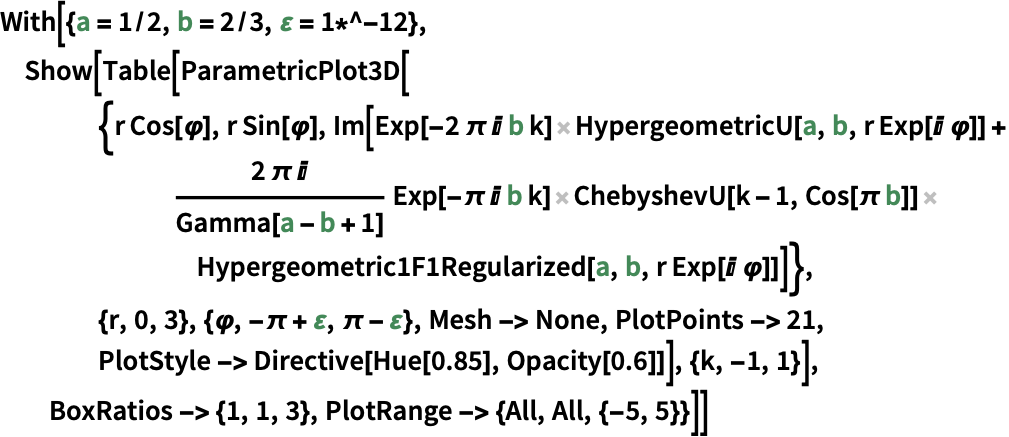HypergeometricU
✖
HypergeometricU

✖

トリコミ合流型超幾何関数 TemplateBox[{a, b, z}, HypergeometricU]である．

詳細

  • 記号操作・数値操作の両方に適した数学関数である．
  • この関数 TemplateBox[{a, b, z}, HypergeometricU]は，積分式 TemplateBox[{a, b, z}, HypergeometricU]=1/TemplateBox[{a}, Gamma]int_0^inftye^(-zt)t^(a-1)(1+t)^(b-a-1) dt を持つ．
  • HypergeometricU[a,b,z]は，複素 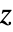平面上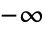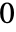，〜の範囲で不連続な分枝切断線を持つ．
  • 特別な引数の場合，HypergeometricUは，自動的に厳密値を計算する．
  • HypergeometricUは任意の数値精度で評価できる．
  • HypergeometricUは自動的にリストに縫い込まれる．
  • HypergeometricUはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる． »

例題

すべて開くすべて閉じる

例  (5)基本的な使用例

数値的に評価する：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-e0aa4
Out[1]=1

実数の部分集合上で をプロットする：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-dizvcm
Out[1]=1

複素数の部分集合上でプロットする：

In[1]:=1
✖
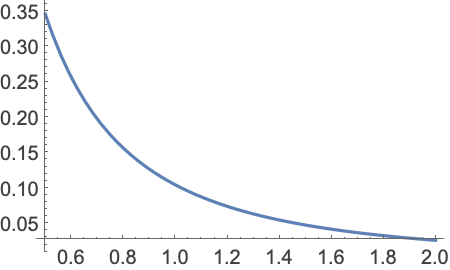
https://wolfram.com/xid/0i1s959p5-kiedlx
Out[1]=1

原点における級数展開：

In[1]:=1
✖
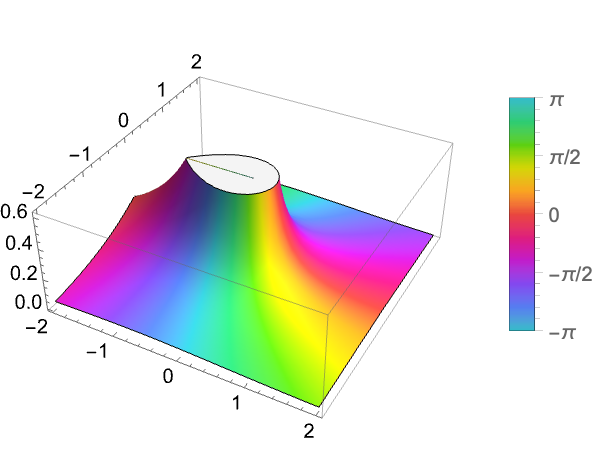
https://wolfram.com/xid/0i1s959p5-mi5s5p
Out[1]=1

Infinityにおける級数展開：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-laddhh
Out[1]=1

スコープ  (39)標準的な使用例のスコープの概要

数値評価  (5)

高精度で評価する：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-cz0ume
Out[1]=1

出力精度は入力精度に従う：

In[2]:=2
✖
https://wolfram.com/xid/0i1s959p5-dke9ki
Out[2]=2

複素引数について評価する：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-dkhrbz
Out[1]=1

HypergeometricUを高精度で効率よく評価する：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-di5gcr
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0i1s959p5-bq2c6r
Out[2]=2

IntervalオブジェクトとCenteredIntervalオブジェクトを使って最悪の場合に保証される区間を計算する：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-cmdnbi
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0i1s959p5-cdcyeo
Out[2]=2

Aroundを使って平均的な場合の統計区間を計算することもできる：

In[3]:=3
✖
https://wolfram.com/xid/0i1s959p5-cw18bq
Out[3]=3

配列の要素ごとの値を計算する：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-thgd2
Out[1]=1

MatrixFunctionを使って行列のHypergeometricU関数を計算することもできる：

In[2]:=2
✖
https://wolfram.com/xid/0i1s959p5-o5jpo
Out[2]=2

特定の値  (3)

HypergeometricUは，ある種のパラメータについては，評価すると自動的により簡単な関数になる：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-npdldt
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0i1s959p5-ckqzfq
Out[2]=2

無限大における極限値：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-m0ibdd
Out[1]=1

方程式 TemplateBox[{3, 2, x}, HypergeometricU]=1を満足する の値を求める：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-f2hrld
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0i1s959p5-gyxup0
Out[2]=2

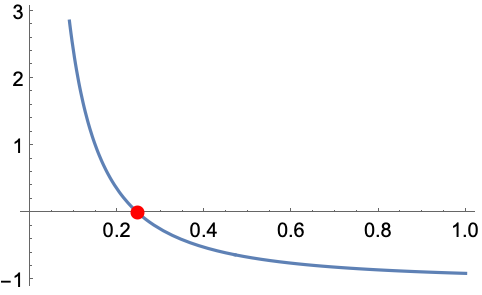
可視化  (3)

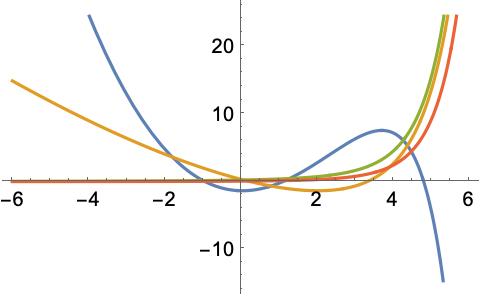
HypergeometricU関数をプロットする：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-ecj8m7
Out[1]=1

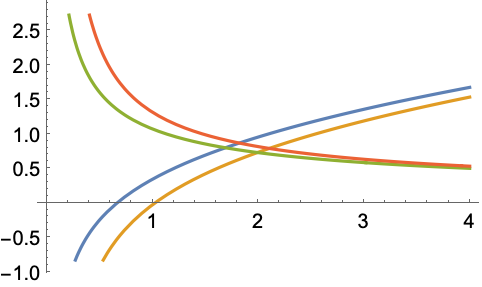
HypergeometricUをその第2パラメータの関数としてプロットする：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-gq0e7
Out[1]=1

TemplateBox[{{1, /, 2}, {sqrt(, 3, )}, z}, HypergeometricU]の実部をプロットする：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-dqlpko
Out[1]=1

TemplateBox[{{1, /, 2}, {sqrt(, 3, )}, z}, HypergeometricU]の虚部をプロットする：

In[2]:=2
✖
https://wolfram.com/xid/0i1s959p5-hhux8h
Out[2]=2

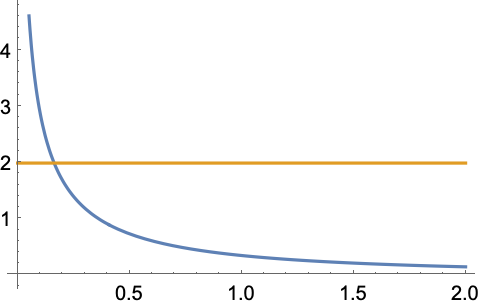
関数の特性  (9)

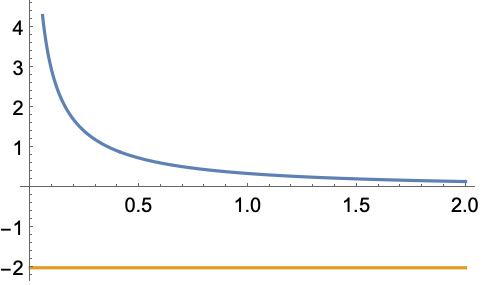
HypergeometricUの実数領域：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-i48j6x
Out[1]=1

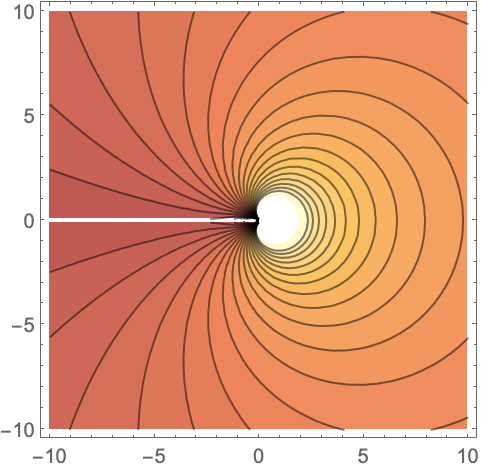
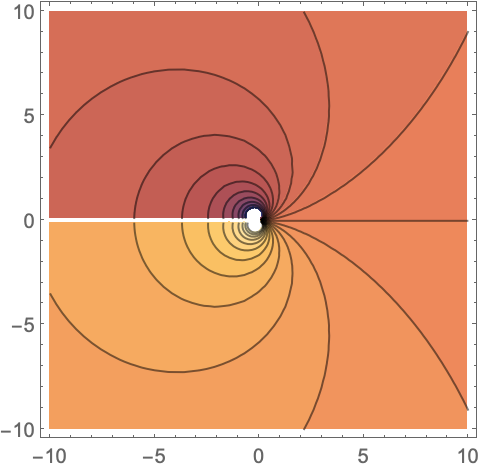
HypergeometricUの複素数領域：

In[2]:=2
✖
https://wolfram.com/xid/0i1s959p5-mbgh6u
Out[2]=2

TemplateBox[{{sqrt(, 3, )}, {sqrt(, 2, )}, z}, HypergeometricU]は解析関数ではない：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-dpcmbc
Out[1]=1

TemplateBox[{{sqrt(, 3, )}, {sqrt(, 2, )}, z}, HypergeometricU]は実領域では非減少でも非増加でもない：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-elzs35
Out[1]=1

TemplateBox[{{sqrt(, 3, )}, {sqrt(, 2, )}, z}, HypergeometricU]は単射である：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-g54sqh
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0i1s959p5-zf7zy
Out[2]=2

TemplateBox[{{sqrt(, 3, )}, {sqrt(, 2, )}, z}, HypergeometricU]は全射ではない：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-klmhpu
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0i1s959p5-b5ts4n
Out[2]=2

TemplateBox[{{sqrt(, 3, )}, {sqrt(, 2, )}, z}, HypergeometricU]は実領域で正である：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-bdbh0f
Out[1]=1

TemplateBox[{{sqrt(, 3, )}, {sqrt(, 2, )}, z}, HypergeometricU]は z≤0のとき特異点と不連続点の両方を持つ：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-hl8oqu
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0i1s959p5-counuv
Out[2]=2

TemplateBox[{{sqrt(, 3, )}, {sqrt(, 2, )}, z}, HypergeometricU]は実領域で凸である：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-7w0foa
Out[1]=1

TraditionalFormによる表示：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-8fepb4

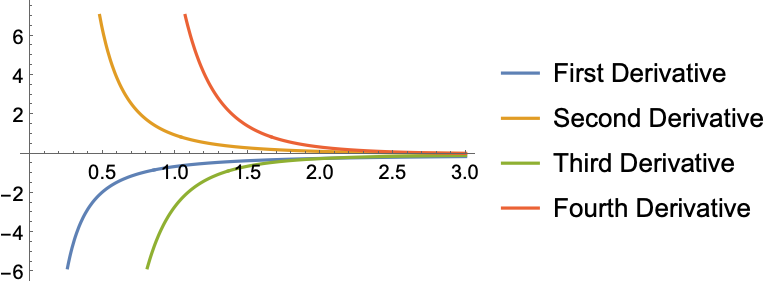
微分  (3)

一次導関数：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-mmas49
Out[1]=1

高次導関数：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-nfbe0l
Out[1]=1

高次導関数を ，についてプロットする：

In[2]:=2
✖
https://wolfram.com/xid/0i1s959p5-fxwmfc
Out[2]=2

次導関数の式：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-odmgl1
Out[1]=1

積分  (3)

HypergeometricUの不定積分：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-bponid
Out[1]=1

HypergeometricUの定積分：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-byhut5
Out[1]=1

その他の積分例：

In[1]:=1
✖
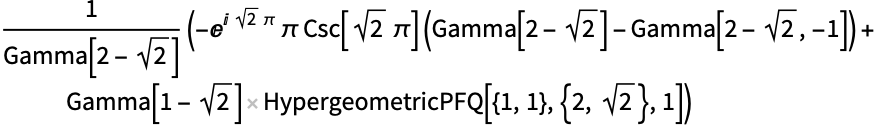
https://wolfram.com/xid/0i1s959p5-iuuysk
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0i1s959p5-e2pjgn
Out[2]=2

級数展開  (3)

HypergeometricUの級数展開：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-ewr1h8
Out[1]=1

の周りの TemplateBox[{{1, /, 2}, {sqrt(, 3, )}, x}, HypergeometricU]の最初の3つの近似をプロットする：

In[5]:=5
✖
https://wolfram.com/xid/0i1s959p5-binhar
Out[6]=6

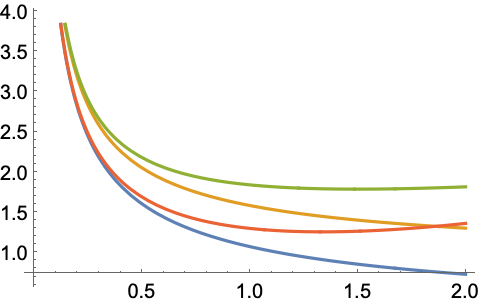
無限大の周囲でHypergeometricUを級数展開する：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-b5ywvs
Out[1]=1

HypergeometricUをベキ級数に適用する：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-br74bf
Out[1]=1

積分変換  (3)

LaplaceTransformを使ってラプラス(Laplace)変換を計算する：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-lrm1i
Out[1]=1

MellinTransform：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-byb4jh
Out[1]=1

HankelTransform：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-bik34q
Out[1]=1

関数の恒等式と簡約  (2)

引数の簡約：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-c5sh5c
Out[1]=1

再帰関係：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-b69p0s
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0i1s959p5-c4q3xf
Out[2]=2

関数表現  (5)

主定義：

In[1]:=1
✖
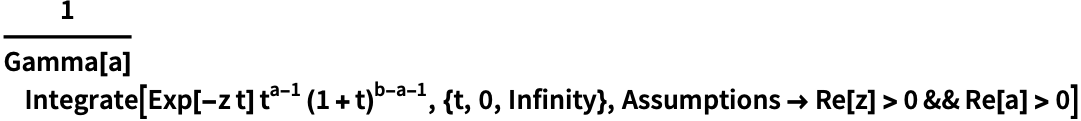
https://wolfram.com/xid/0i1s959p5-btrz2h
Out[1]=1

GammaとHypergeometric1F1を介した表現：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-jsway7
Out[1]=1

HypergeometricUはMeijerGによって表すことができる：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-c3r3u
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0i1s959p5-cqbusy
Out[2]=2

HypergeometricUはDifferentialRootとして表すことができる：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-xf52z
Out[1]=1

TraditionalFormによる表示：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-g0745t

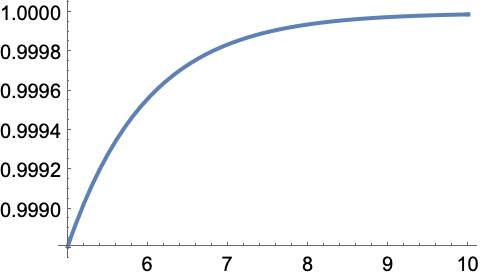
アプリケーション  (3)この関数で解くことのできる問題の例

合流型超幾何微分方程式を解く：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-gi2zn
Out[1]=1

関数の発散級数についてのボレル(Borel)の総和はHypergeometricUを返す：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-cq97n4
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0i1s959p5-dminu8
Out[2]=2

SumのRegularizationオプションを使っても同じ結果を得ることができる：

In[3]:=3
✖
https://wolfram.com/xid/0i1s959p5-idkg8w
Out[3]=3

WishartMatrixDistributionのスケールされた条件数についての分布を定義する：

In[1]:=1
✖
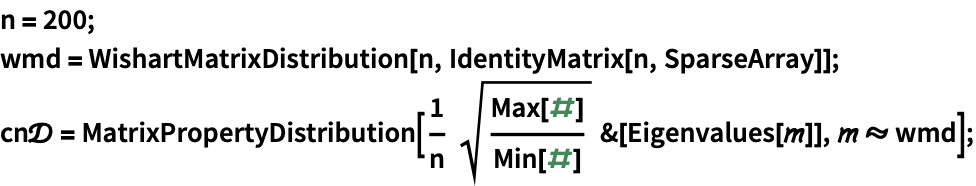
https://wolfram.com/xid/0i1s959p5-f8ju8d

大きい行列のスケールされた条件数のサンプルを取り，これが漸近的な閉じた形の分布と一致することを確認する：

In[2]:=2
✖
https://wolfram.com/xid/0i1s959p5-dmxnus
In[3]:=3
✖
https://wolfram.com/xid/0i1s959p5-dkrzl7
In[4]:=4
✖
https://wolfram.com/xid/0i1s959p5-m5iijt
Out[4]=4

漸近的なスケールされた条件数分布は無限平均を持つ：

In[5]:=5
✖
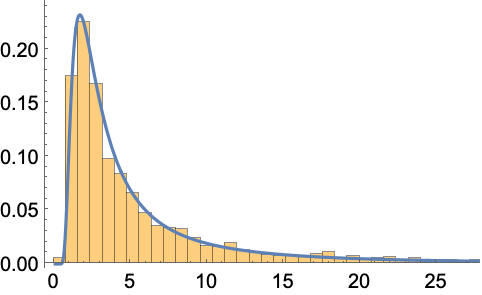
https://wolfram.com/xid/0i1s959p5-52na7
Out[5]=5
In[6]:=6
✖
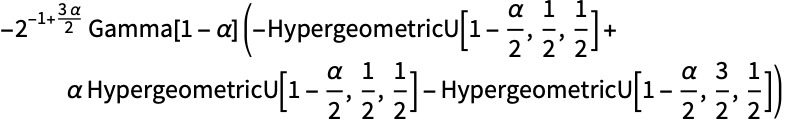
https://wolfram.com/xid/0i1s959p5-f4gfmu
Out[6]=6

特性と関係  (4)この関数の特性および他の関数との関係

FunctionExpandを使ってHypergeometricUをより簡単な関数に展開する：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-gcnabe
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0i1s959p5-dpvijd
Out[2]=2

IntegrateはHypergeometricUを含む結果を返すことがある：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-col0t5
Out[1]=1

HypergeometricUはDifferentialRootとして表すことができる：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-ddbh2
Out[1]=1

HypergeometricUはDifferenceRootとして表すことができる：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-cjx8vb
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0i1s959p5-ojcks5
Out[2]=2

考えられる問題  (1)よく起る問題と予期しない動作

$MaxExtraPrecisionのデフォルトの設定値では所望精度を得るのには不十分かもしれない：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-mjshgb
Out[1]=1

$MaxExtraPrecisionの設定値を大きくする必要があるかもしれない：

In[2]:=2
✖
https://wolfram.com/xid/0i1s959p5-d6e6sm
Out[2]=2

おもしろい例題  (2)驚くような使用例や興味深い使用例

合流関係TemplateBox[{TemplateBox[{a, {a, -, b, +, 1}, c, {1, -, {c, /, z}}}, Hypergeometric2F1], c, infty}, Limit2Arg]z^(-a)=TemplateBox[{a, b, z}, HypergeometricU]を可視化する：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-9p0bvc
Out[1]=1

TemplateBox[{{1, /, 2}, {2, /, 3}, z}, HypergeometricU]のリーマン(Riemann)面をプロットする：

In[1]:=1
✖
https://wolfram.com/xid/0i1s959p5-j6sstg
Out[1]=1
Wolfram Research (1988), HypergeometricU, Wolfram言語関数， https://reference.wolfram.com/language/ref/HypergeometricU.html （2022年に更新）.
✖
Wolfram Research (1988), HypergeometricU, Wolfram言語関数， https://reference.wolfram.com/language/ref/HypergeometricU.html （2022年に更新）.

テキスト

Wolfram Research (1988), HypergeometricU, Wolfram言語関数， https://reference.wolfram.com/language/ref/HypergeometricU.html （2022年に更新）.

✖
Wolfram Research (1988), HypergeometricU, Wolfram言語関数， https://reference.wolfram.com/language/ref/HypergeometricU.html （2022年に更新）.

CMS

Wolfram Language. 1988. "HypergeometricU." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/HypergeometricU.html.

✖
Wolfram Language. 1988. "HypergeometricU." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/HypergeometricU.html.

APA

Wolfram Language. (1988). HypergeometricU. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HypergeometricU.html

✖
Wolfram Language. (1988). HypergeometricU. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HypergeometricU.html

BibTeX

@misc{reference.wolfram_2025_hypergeometricu, author="Wolfram Research", title="{HypergeometricU}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/HypergeometricU.html}", note=[Accessed: 17-April-2025 ]}

✖
@misc{reference.wolfram_2025_hypergeometricu, author="Wolfram Research", title="{HypergeometricU}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/HypergeometricU.html}", note=[Accessed: 17-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_hypergeometricu, organization={Wolfram Research}, title={HypergeometricU}, year={2022}, url={https://reference.wolfram.com/language/ref/HypergeometricU.html}, note=[Accessed: 17-April-2025 ]}

✖
@online{reference.wolfram_2025_hypergeometricu, organization={Wolfram Research}, title={HypergeometricU}, year={2022}, url={https://reference.wolfram.com/language/ref/HypergeometricU.html}, note=[Accessed: 17-April-2025 ]}