Interpolation

Interpolation[{f1,f2,…}]

x の値1, 2, … に対応すると思われる関数の値 fiを補間する．

Interpolation[{{x1,f1},{x2,f2},…}]

x の値 xiに対応する関数の値 fiを補間する．

Interpolation[{{{x1,y1,…},f1},{{x2,y2,…},f2},…}]

多次元データを補間する．

Interpolation[{{{x1,…},f1,df1,…},…}]

関数の値とともに導関数も再生する補間を行う．

Interpolation[data,x]

点 x でデータ data の補間を求める．

詳細とオプション

  • Interpolationは他の純関数と同じように使えるInterpolatingFunctionオブジェクトを返す．
  • Interpolation[data]によって返された補間関数は，data によって明示的に指定されたすべての点における data と一致するように設定されている．
  • 関数の値 fiは実数，複素数，任意の記号式のいずれでもよい．
  • fiはリストでも任意の次元の配列でもよい．
  • 関数の引数 xi, yi等は実数でなければならない．
  • データ中の異なる要素は指定された異なる数の導関数を持つことができる．
  • 多次元データについて，D[f,{{x,y,…},n}]に対応するテンソルとして n 次導関数を与えることができる．
  • 明示的に指定されていない偏微分はAutomaticとして与えることができる．
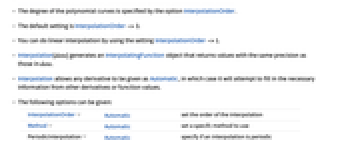
  • Interpolationは，多項式曲線を一連のデータ点に適合させるように機能する．
  • 多項式曲線の次数は，オプションInterpolationOrderで指定される．
  • このデフォルト設定は，InterpolationOrder->3である．
  • InterpolationOrder->1を使って，線形な補間を行うことができる．
  • Interpolation[data]は，InterpolatingFunctionオブジェクト生成し，data と同じ精度を使った値が返される．
  • Interpolationでは，任意の導関数をAutomaticとして与えることができる．この場合，必要な情報は，他の導関数あるいは関数値から得ようと試みられる．
  • 次は，使用可能なオプションである．
  • InterpolationOrder Automatic補間順序を設定する
    Method Automatic使用する特定のメソッドを設定する
    PeriodicInterpolation Automatic補間が周期的かどうかを指定する
  • InterpolationはMethodオプションをサポートする．使用可能な設定値としてはスプライン補間には"Spline"，エルミート補間には"Hermite"がある．

例題

すべて開くすべて閉じる

例  (2)

データを補間する近似関数を構築する：

関数を適用して補間値を求める：

補間関数をプロットする：

もとのデータと比べる：

補間された値を直ちに求める：

スコープ  (4)

任意の の値における点の間を補間する：

Tableを使ってデータを作成する：

補間する：

補間した関数をプロットする：

多次元データのリストを作成する：

近似補間関数を作成する：

補間関数をプロットする：

TimeSeriesとして与えられるデータから補間する：

補間された関数をプロットする：

一般化と拡張  (5)

各点における導関数を含むデータを作成する：

補間を構築する：

補間をプロットする：

各点における傾斜ベクトルを含む二元データを作成する：

傾斜を含まないデータと比較する：

二次導関数のテンソルも含ませる：

ベクトル値データから1変数のベクトル値InterpolatingFunctionを作る：

値はベクトルである：

Plotは両方の成分を表示する：

ベクトル値データから2変数のベクトル値InterpolatingFunctionを作る：

値はベクトルである：

Plot3Dは3成分すべてを表示する：

Partを使って1成分だけプロットすることもできる：

エルミート補間には導関数を含めることもできる：

オプション  (5)

InterpolationOrder  (3)

次数ゼロの補間を行う：

線形補間を行う：

二次補間を行う：

Method  (1)

ランダムなデータの区分エルミート補間とスプライン補間を比較する：

曲線は接近しているように見えるが，スプラインの方は連続する導関数を持つ：

PeriodicInterpolation  (1)

周期的に繰り返す補間関数を作成する：

アプリケーション  (2)

ランダムなデータを補間する：

GCD関数の連続補間を求める：

特性と関係  (2)

補間関数は常にデータ点を通る：

補間関数の積分を求める：

補間関数とその積分をプロットする：

考えられる問題  (3)

外挿はもとのデータを超えた範囲を試みる：

デフォルトの次数選択では，少なくとも各次元に4点必要である：

次数を低くすると，必要な点の数も少なくなる：

補間関数は常に連続的であるが，微分できるとは限らない：

おもしろい例題  (1)

一連の素数を補間する：

Wolfram Research (1991), Interpolation, Wolfram言語関数， https://reference.wolfram.com/language/ref/Interpolation.html （2008年に更新）.

テキスト

Wolfram Research (1991), Interpolation, Wolfram言語関数， https://reference.wolfram.com/language/ref/Interpolation.html （2008年に更新）.

CMS

Wolfram Language. 1991. "Interpolation." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2008. https://reference.wolfram.com/language/ref/Interpolation.html.

APA

Wolfram Language. (1991). Interpolation. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Interpolation.html

BibTeX

@misc{reference.wolfram_2024_interpolation, author="Wolfram Research", title="{Interpolation}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/Interpolation.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_interpolation, organization={Wolfram Research}, title={Interpolation}, year={2008}, url={https://reference.wolfram.com/language/ref/Interpolation.html}, note=[Accessed: 18-November-2024 ]}