Interpolation
Interpolation[{f1,f2,…}]
对应 x 值 1、2、… ,构造函数值 fi 的插值.
Interpolation[{{x1,f1},{x2,f2},…}]
对应 x 的值 xi,构造函数值 fi 的插值.
Interpolation[{{{x1,y1,…},f1},{{x2,y2,…},f2},…}]
构造多维数据的插值.
Interpolation[{{{x1,…},f1,df1,…},…}]
构造一个插值,再现导数及函数值.
Interpolation[data,x]
在点 x 求 data 的插值.
更多信息和选项

- Interpolation 返回一个 InterpolatingFunction 对象,它可以同其它纯函数一样使用.
- Interpolation[data] 返回的插值函数与每个点处的 data 一致.
- 函数值 fi 可以是实数、复数或任意符号表达式.
- fi 可以是列表或任意维度的阵列.
- 函数参数 xi、yi 等必须是实数.
- 数据内不同的元素可以有不同数量的指定导数.
- 对于多维数据,n
 阶导数可以作为一个对应 D[f,{{x,y,…},n}] 的结构的张量给出.
阶导数可以作为一个对应 D[f,{{x,y,…},n}] 的结构的张量给出. - 未被显式指定的偏导数可以以 Automatic 给出.
- Interpolation 的算法是在连续数据点间拟合多项式曲线.
- 多项式曲线的次数由选项 InterpolationOrder 指定.
- 默认设置是 InterpolationOrder->3.
- 可以通过使用设置 InterpolationOrder->1 进行线性插值.
- Interpolation[data] 生成 InterpolatingFunction 对象,该对象返回和 data 中的值有相同精度的值.
- Interpolation 允许任何导数以 Automatic 给出,在这些情况下,它会尽量填充从其它导数或函数值获得的信息.
- Interpolation 支持 Method 选项. 可能的设置包括表示样条插值的 "Spline" 和厄米特插值的 "Hermite".
范例
打开所有单元关闭所有单元范围 (4)
创建 Table 的数据:
根据以 TimeSeries 形式给出的数据形成插值:
推广和延伸 (5)
根据向量值数据,创建一个变量的向量值 InterpolatingFunction:
Plot 会显示两个分量:
根据向量值数据创建两个变量的向量值 InterpolatingFunction:
Plot3D 会显示所有三个分量:
单个分量可以使用 Part 绘制:
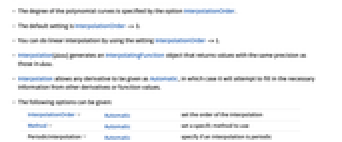
选项 (5)
文本
Wolfram Research (1991),Interpolation,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Interpolation.html (更新于 2008 年).
CMS
Wolfram 语言. 1991. "Interpolation." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2008. https://reference.wolfram.com/language/ref/Interpolation.html.
APA
Wolfram 语言. (1991). Interpolation. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Interpolation.html 年