InverseBilateralZTransform

InverseBilateralZTransform[expr,z,n]

gives the inverse bilateral Z transform of expr.

InverseBilateralZTransform[expr,{z1,…,zk},{n1,…,nk}]

gives the multidimensional inverse bilateral Z transform of expr.

Details and Options

  • The inverse bilateral Z transform provides the map from Fourier space back to state space, and allows one to recover the original sequence in applications of the bilateral Z transform.
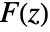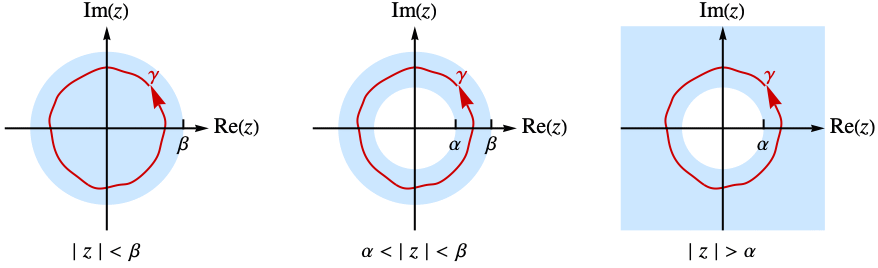
  • The inverse bilateral Z transform of a function is given by the contour integral 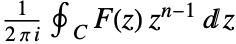, where the integration is along a counterclockwise contour 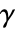, lying in an annulus alpha<TemplateBox[{z}, Abs]<beta in which the function 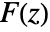is holomorphic. In some cases, the annulus of analyticity may extend to the interior or the exterior of a disk.
  • The multidimensional inverse transform is given by 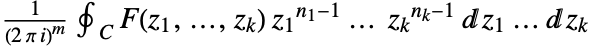, where .
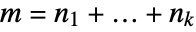  • The following options can be given:
  • AccuracyGoalAutomaticdigits of absolute accuracy sought
    Assumptions $Assumptionsassumptions to make about parameters
    GenerateConditionsFalsewhether to generate answers that involve conditions on parameters
    MethodAutomaticmethod to use
    PerformanceGoal$PerformanceGoalaspects of performance to optimize
    PrecisionGoalAutomaticdigits of precision sought
    WorkingPrecision Automaticthe precision used in internal computations

Examples

open allclose all

Basic Examples  (5)

Inverse bilateral Z transform of a rational function defined in an annulus:

Compute the inverse transform at a single point:

Function defined in the exterior of a disk:

Function defined in the interior of a disk:

Function with an essential singularity at zero:

Multivariate inverse bilateral transform:

Scope  (7)

Shifted impulse sequences:

Rational functions yield exponential and trigonometric sequences:

Functions involving parameters:

The following function defined in the interior of a circle leads to a trigonometric sequence:

If the ROC is not provided, then it is assumed to be the region containing all the function poles:

Obtain the same result using InverseZTransform:

Calculate the inverse bilateral Z transform at a single point using a numerical method:

Alternatively, calculate inverse symbolically:

Then evaluate it for a specific value of :

For some functions, the inverse bilateral Z transform can be evaluated only numerically:

Plot the inverse bilateral Z transform using numerical values only:

Options  (2)

Assumptions  (1)

Use Assumptions to restrict the parameter domain:

WorkingPrecision  (1)

Use WorkingPrecision to obtain a result with arbitrary precision:

Applications  (2)

Define finite duration and exponentially decaying signals:

Plot signals in the time domain:

To find the convolution, first calculate product of the transforms:

Then, perform inversion back to the time domain:

Plot the convolution in the time domain:

Alternatively, find the convolution using DiscreteConvolve:

Define a pair of infinite duration signals:

Plot the signals in the time domain:

To find the convolution, first calculate the product of the transforms:

Perform inversion back to the time domain:

Plot the convolution in the time domain:

Alternatively, find the convolution using DiscreteConvolve:

Properties & Relations  (4)

Relation to BilateralZTransform:

InverseBilateralZTransform is closely related to InverseFourierSequenceTransform:

Linearity:

Scaling:

Possible Issues  (1)

No poles are allowed in the region of convergence:

Neat Examples  (1)

Create a table of basic inverse bilateral Z transforms:

Wolfram Research (2021), InverseBilateralZTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseBilateralZTransform.html.

Text

Wolfram Research (2021), InverseBilateralZTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseBilateralZTransform.html.

CMS

Wolfram Language. 2021. "InverseBilateralZTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InverseBilateralZTransform.html.

APA

Wolfram Language. (2021). InverseBilateralZTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseBilateralZTransform.html

BibTeX

@misc{reference.wolfram_2025_inversebilateralztransform, author="Wolfram Research", title="{InverseBilateralZTransform}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/InverseBilateralZTransform.html}", note=[Accessed: 21-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_inversebilateralztransform, organization={Wolfram Research}, title={InverseBilateralZTransform}, year={2021}, url={https://reference.wolfram.com/language/ref/InverseBilateralZTransform.html}, note=[Accessed: 21-February-2025 ]}