InverseZTransform[expr,z,n]
gives the inverse Z transform of expr.
InverseZTransform[expr,{z1,…,zm},{n1,…,nm}]
gives the multiple inverse Z transform of expr.


InverseZTransform
InverseZTransform[expr,z,n]
gives the inverse Z transform of expr.
InverseZTransform[expr,{z1,…,zm},{n1,…,nm}]
gives the multiple inverse Z transform of expr.
Details and Options
- The inverse Z transform of a function
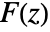 is given by the contour integral
is given by the contour integral 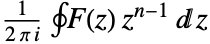 .
. - The multidimensional inverse Z transform is given by
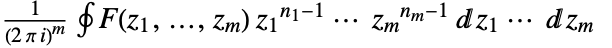 .
. - The following options can be given:
-
Assumptions $Assumptions assumptions to make about parameters Method Automatic method to use - In TraditionalForm, InverseZTransform is output using
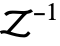 .
.
Examples
open all close allScope (4)
Options (1)
Assumptions (1)
This transform will not evaluate without any constraints on the range of p:
Use Assumptions to limit the range of p:
Applications (3)
Solve a linear difference equation:
Add an initial value equation and solve the algebraic equation for the transform:
Get the solution through inverse transformation:
Use RSolve:
Solve a linear difference-summation equation:
Use the inverse transform to get a solution to the original problem:
Use RSolve:
Properties & Relations (6)
Use DiscreteAsymptotic to compute an asymptotic approximation:
ZTransform is the inverse operator:
InverseZTransform is closely related to SeriesCoefficient:
Tech Notes
Related Guides
Related Links
History
Introduced in 1999 (4.0) | Updated in 2008 (7.0)
Text
Wolfram Research (1999), InverseZTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseZTransform.html (updated 2008).
CMS
Wolfram Language. 1999. "InverseZTransform." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2008. https://reference.wolfram.com/language/ref/InverseZTransform.html.
APA
Wolfram Language. (1999). InverseZTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseZTransform.html
BibTeX
@misc{reference.wolfram_2025_inverseztransform, author="Wolfram Research", title="{InverseZTransform}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/InverseZTransform.html}", note=[Accessed: 18-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_inverseztransform, organization={Wolfram Research}, title={InverseZTransform}, year={2008}, url={https://reference.wolfram.com/language/ref/InverseZTransform.html}, note=[Accessed: 18-January-2026]}