InverseBilateralZTransform

InverseBilateralZTransform[expr,z,n]

expr の逆両側Z変換を与える．

InverseBilateralZTransform[expr,{z1,…,zk},{n1,…,nk}]

expr の多次元逆両側Z変換を与える．

詳細とオプション

  • 逆両側Z変換はフーリエ(Fourier)空間から状態空間への写像を与え，両側Z変換の適用でもとの列が回復できる．
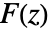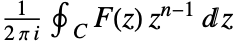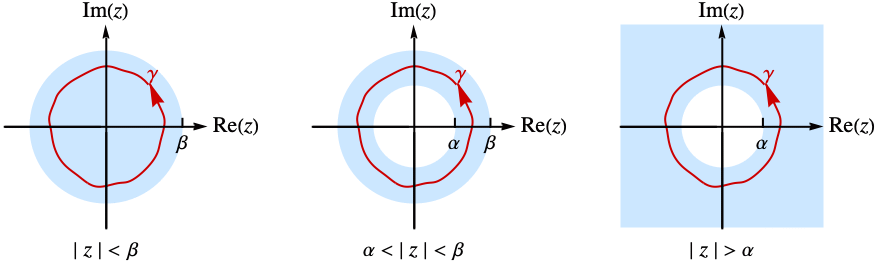
  • 関数 の逆両側Z変換は周回積分 で与えられる．積分は，関数 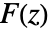が正則であるアニュラス alpha<TemplateBox[{z}, Abs]<beta 内にある等高線 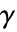に沿って反時計回りに行われる．場合によっては解析性のアニュラスが円板の外側あるいは内側に拡張されるかもしれない．
  • 多次元逆変換は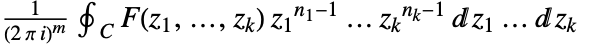で与えられる．ただし 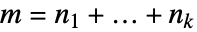である．
  • 次は，使用可能なオプションである．
  • AccuracyGoalAutomatic目的とする絶対確度の桁数
    Assumptions $Assumptionsパタメータについての仮定
    GenerateConditionsFalseパラメータについての条件を含む答を生成するかどうか
    MethodAutomatic使用するメソッド
    PerformanceGoal$PerformanceGoal何を最適化するか
    PrecisionGoalAutomatic目的精度の桁数
    WorkingPrecision Automatic内部計算精度

例題

すべて開くすべて閉じる

例  (5)

アニュラスで定義された有理関数の逆両側Z変換：

単一の点における逆変換を計算する：

円板の外側で定義された関数：

円板の内側で定義された関数：

0に真性特異点を持つ関数：

多変量逆両側変換：

スコープ  (7)

シフトされたインパルス列：

有理関数は指数関数列と三角関数列を返す：

パラメータを含む関数：

円の内側で定義された次の関数は三角関数列を返す：

曲率半径は，与えられなければ関数のすべての極を含む領域であると仮定される：

InverseZTransformを使って同じ結果を得る：

数値法を使って単一の点で逆両側Z変換を計算する：

逆変換を記号的に計算することもできる：

次に， の特定の値で評価する：

関数によっては逆両側Z変換が数値的にしか評価できないものもある：

数値だけを使って逆両側Z変換をプロットする：

オプション  (2)

Assumptions  (1)

Assumptionsを使ってパラメータの領域を制限する：

WorkingPrecision  (1)

WorkingPrecisionを使って結果を任意精度で得る：

アプリケーション  (2)

有限持続で指数関数的に減衰する信号を定義する：

信号を時間領域でプロットする：

たたみ込みが求めたければ，まず変換の積を計算する：

次に，時間領域に反転し直す：

たたみ込みを時間領域でプロットする：

DiscreteConvolveを使ってたたみ込みを求めることもできる：

無限時間信号のペアを定義する：

信号を時間領域でプロットする：

たたみ込みが求めたければ，まず変換の積を計算する：

時間領域に反転し直す：

たたみ込みを時間領域でプロットする：

DiscreteConvolveを使ってたたみ込みを求めることもできる：

特性と関係  (4)

BilateralZTransformとの関係：

InverseBilateralZTransformはInverseFourierSequenceTransformと密接な関係がある：

線形性：

スケーリング：

考えられる問題  (1)

収束領域には極があってはならない：

おもしろい例題  (1)

基本的な逆両側Z変換の表を作る：

Wolfram Research (2021), InverseBilateralZTransform, Wolfram言語関数， https://reference.wolfram.com/language/ref/InverseBilateralZTransform.html.

テキスト

Wolfram Research (2021), InverseBilateralZTransform, Wolfram言語関数， https://reference.wolfram.com/language/ref/InverseBilateralZTransform.html.

CMS

Wolfram Language. 2021. "InverseBilateralZTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InverseBilateralZTransform.html.

APA

Wolfram Language. (2021). InverseBilateralZTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseBilateralZTransform.html

BibTeX

@misc{reference.wolfram_2024_inversebilateralztransform, author="Wolfram Research", title="{InverseBilateralZTransform}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/InverseBilateralZTransform.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_inversebilateralztransform, organization={Wolfram Research}, title={InverseBilateralZTransform}, year={2021}, url={https://reference.wolfram.com/language/ref/InverseBilateralZTransform.html}, note=[Accessed: 21-November-2024 ]}