InverseBilateralZTransform
InverseBilateralZTransform[expr,z,n]
给出 expr 的逆双边 Z 变换.
InverseBilateralZTransform[expr,{z1,…,zk},{n1,…,nk}]
给出 expr 的多维逆双边 Z 变换.
更多信息和选项

- 逆双边 Z 变换提供了从傅立叶空间回到状态空间的映射,并允许在双边 Z 变换的应用中恢复原始序列.
- 函数
 的逆双边 Z 变换由围线积分
的逆双边 Z 变换由围线积分 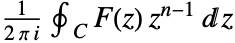 给出,其中积分沿逆时针围线
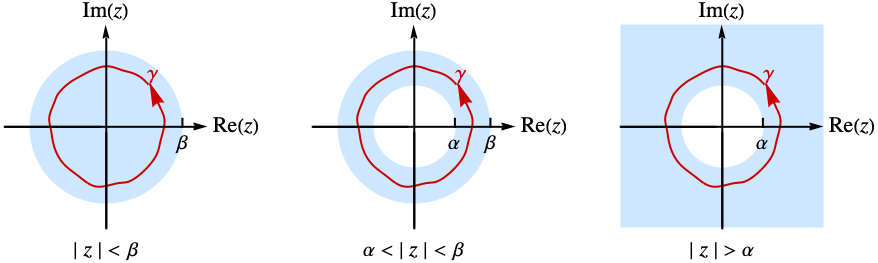
给出,其中积分沿逆时针围线 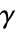 ,位于环
,位于环 ![alpha<TemplateBox[{z}, Abs]<beta alpha<TemplateBox[{z}, Abs]<beta](Files/InverseBilateralZTransform.zh/4.png) 中,其中函数
中,其中函数 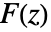 是全纯函数. 在某些情况下,分析环可能会延伸到圆盘的内部或外部.
是全纯函数. 在某些情况下,分析环可能会延伸到圆盘的内部或外部. - 多维逆变换由
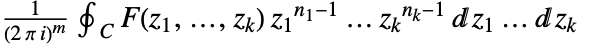 给出,其中
给出,其中 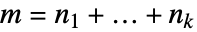 .
. - 可以提供以下选项:
-
AccuracyGoal Automatic 所寻求的绝对精度的数位 Assumptions $Assumptions 对参数所作的假设 GenerateConditions False 是否生成涉及参数条件的答案 Method Automatic 使用方法 PerformanceGoal $PerformanceGoal 要优化的性能方面 PrecisionGoal Automatic 所寻求的精度的数位 WorkingPrecision Automatic 内部计算中使用的精度
范例
打开所有单元关闭所有单元范围 (7)
使用 InverseZTransform 获得相同的结果:
选项 (2)
Assumptions (1)
使用 Assumptions 限制参数域:
WorkingPrecision (1)
使用 WorkingPrecision 获得任意精度的结果:
应用 (2)
或者,使用 DiscreteConvolve 求卷积:
或者,使用 DiscreteConvolve 求卷积:
属性和关系 (4)
Wolfram Research (2021),InverseBilateralZTransform,Wolfram 语言函数,https://reference.wolfram.com/language/ref/InverseBilateralZTransform.html.
文本
Wolfram Research (2021),InverseBilateralZTransform,Wolfram 语言函数,https://reference.wolfram.com/language/ref/InverseBilateralZTransform.html.
CMS
Wolfram 语言. 2021. "InverseBilateralZTransform." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/InverseBilateralZTransform.html.
APA
Wolfram 语言. (2021). InverseBilateralZTransform. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/InverseBilateralZTransform.html 年