WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

InverseErf[s]

での z の解として求まる逆誤差関数を与える．

詳細
Details and Options Details and Options
例題  
例  
スコープ  
数値評価  
特定の値  
可視化  
Show More Show More
関数の特性  
微分  
積分  
級数展開  
関数の恒等式と簡約  
関数表現  
アプリケーション  
特性と関係  
考えられる問題  
おもしろい例題  
関連項目
テクニカルノート
関連するガイド
関連リンク
履歴
引用書式

InverseErf

InverseErf[s]

での z の解として求まる逆誤差関数を与える．

詳細

  • 記号操作・数値操作の両方に適した数学関数である．
  • 明示的な数値として求まるのは，s が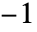から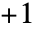の範囲の実数の値を取るときに限る．
  • InverseErf[z0,s]は，一般化された誤差関数Erf[z0,z]の逆誤差関数を与える．
  • 特別な引数の場合，InverseErfは，自動的に厳密値を計算する．
  • InverseErfは任意の数値精度で評価できる．
  • InverseErfは，IntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる． »
  • InverseErfは自動的にリストに縫い込まれる．

例題

すべて開く すべて閉じる

例  (4)

数値的に評価する：

実数の部分集合上でプロットする：

原点における級数展開：

特異点における級数展開：

スコープ  (32)

数値評価  (5)

高精度で数値的に評価する：

出力の精度は入力の精度に従う：

InverseErfを高精度で効率よく評価する：

一般化された逆誤差関数を数値的に評価する：

IntervalオブジェクトとCenteredIntervalオブジェクトを使って最悪の場合に保証される区間を計算する：

Aroundを使って平均的な場合の統計区間を計算することもできる：

配列の要素ごとの値を計算する：

MatrixFunctionを使って行列のInverseErf関数を計算することもできる：

特定の値  (2)

特定の引数についての厳密な結果：

方程式の実根を求める：

可視化  (3)

InverseErf関数をプロットする：

一般化された逆誤差関数を，のさまざまな値についてプロットする：

一般化された逆誤差関数を， のさまざまな値についてプロットする：

関数の特性  (9)

InverseErfは，区間()からのすべての実数値について定義される：

InverseErfはすべての実数値を取る：

InverseErfは奇関数である：

InverseErfはその定義域において解析関数である：

特異点と不連続点の両方を持つので一般的には解析的ではない：

InverseErfはその定義域において非減少である：

InverseErfは単射である：

InverseErfは全射ではない：

InverseErfは非負でも非正でもない：

InverseErfはその定義域において凸でも凹でもない：

微分  (2)

一次導関数：

高次導関数：

積分  (3)

InverseErfの不定積分：

InverseErfの，その実領域上での定積分：

InverseErfの定積分の数値近似：

級数展開  (2)

InverseErfのテイラー(Taylor)展開：

の周りのInverseErfの最初の3つの近似をプロットする：

一般化された逆誤差関数の級数展開：

関数の恒等式と簡約  (2)

逆誤差関数で構築する：

一般化された逆誤差関数で構築する：

関数表現  (4)

逆誤差関数の主定義：

一般化された逆誤差関数との関係：

逆相補誤差関数との関係：

TraditionalFormによる表示：

アプリケーション  (3)

ガウス(Gauss)分布の乱数を生成する：

ガウス分布における99%の信頼区間の標準偏差の数：

InverseErfをプロットする：

特性と関係  (5)

超越方程式を解く：

超越方程式の根を数値的に求める：

微分方程式の解としてInverseErfを求める：

InverseErfは数値関数である：

TraditionalFormでは，は自動的に逆誤差関数と解釈される：

考えられる問題  (1)

InverseErfは，のときにのみ，数値的に評価できる：

おもしろい例題  (1)

InverseErfのリーマン(Riemann)面：

Wolfram Research (1996), InverseErf, Wolfram言語関数， https://reference.wolfram.com/language/ref/InverseErf.html （2023年に更新）.

テキスト

Wolfram Research (1996), InverseErf, Wolfram言語関数， https://reference.wolfram.com/language/ref/InverseErf.html （2023年に更新）.

CMS

Wolfram Language. 1996. "InverseErf." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/InverseErf.html.

APA

Wolfram Language. (1996). InverseErf. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseErf.html

BibTeX

@misc{reference.wolfram_2025_inverseerf, author="Wolfram Research", title="{InverseErf}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/InverseErf.html}", note=[Accessed: 05-October-2025]}

BibLaTeX

@online{reference.wolfram_2025_inverseerf, organization={Wolfram Research}, title={InverseErf}, year={2023}, url={https://reference.wolfram.com/language/ref/InverseErf.html}, note=[Accessed: 05-October-2025]}