KernelMixtureDistribution

KernelMixtureDistribution[{x1,x2,…}]

データ値 xiに基づいたカーネル混合分布を表す．

KernelMixtureDistribution[{{x1,y1,…},{x2,y2,…},…}]

データ値{xi,yi,…}に基づいた多変量カーネル混合分布を表す．

KernelMixtureDistribution[…,bw]

帯域幅が bw のカーネル混合分布を表す．

KernelMixtureDistribution[…,bw,ker]

帯域幅が bw，平滑化カーネルが ker のカーネル混合分布を表す．

詳細とオプション

  • KernelMixtureDistributionは他の確率分布と同じように使えるDataDistributionオブジェクトを返す．
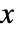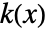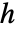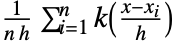  • 値 についてのKernelMixtureDistributionの確率密度関数は，平滑化カーネル ，帯域幅母数 ではで与えられる．
  • 使用可能な帯域幅指定 bw
  • h使用する帯域幅
    {"Standardized",h}標準偏差の単位による帯域幅
    {"Adaptive",h,s}初期帯域幅 h，感度 s の適応的帯域幅
    Automatic自動計算された帯域幅
    "name"名前付き帯域幅選択法を使う
    {bwx,bwy,…}x, y 等に別々の帯域幅指定
  • 多変量密度については，h は正定値対称行列でもよい．
  • 適応的帯域幅については，感度 s は0から1までの実数あるいはAutomaticでなければならない．Automaticの場合，s は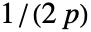に設定される．ただし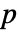， はデータの次元である．
  • 使用可能な名前付き帯域幅選択法
  • "LeastSquaresCrossValidation"最小二乗交差検定法を使う
    "Oversmooth"標準Gaussianの1.08倍広い
    "Scott"Scottの規則を使った帯域幅選択
    "SheatherJones"Sheather–Jonesプラグイン推定器を使う
    "Silverman"Silvermanの規則を使った帯域幅の決定
    "StandardDeviation"帯域幅として標準偏差を使う
    "StandardGaussian"標準正規データの最適帯域幅
  • デフォルトで"Silverman"メソッドが使われる．
  • 帯域幅の自動計算では，定配列が単位分散を持つものとみなされる．
  • 次のカーネル指定 ker が使える．
  • "Biweight"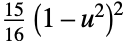
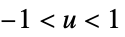
    "Cosine"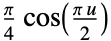
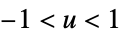
    "Epanechnikov"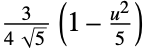
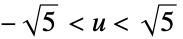
    "Gaussian"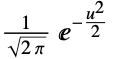
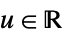
    "Rectangular"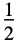
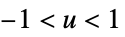
    "SemiCircle"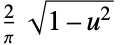
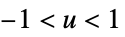
    "Triangular"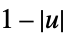
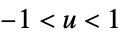
    "Triweight"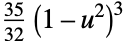
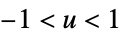
    func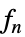f_nu in R
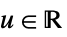
  • KernelMixtureDistributionが真の密度推定を生成するためには，関数 fn は有効な一変量確率密度関数でなければならない．
  • デフォルトで"Gaussian"カーネルが使われる．
  • 多変量密度については，カーネル関数 ker は積およびラジアルタイプとしてそれぞれ{"Product",ker}と{"Radial",ker}を使って指定することができる．積タイプのカーネルはタイプの指定がない場合に使われる．
  • 密度推定に使われる精度は bw とデータで与えられる最低精度である．
  • 使用可能なオプション
  • MaxMixtureKernels Automatic使用するカーネルの最大数
  • KernelMixtureDistributionはMean，CDF，RandomVariate等の関数で使うことができる．

例題

すべて開くすべて閉じる

例  (3)

一変量データのカーネル密度推定を行う：

結果の分布を使って分布関数の可視化を含む分析を行う：

モーメントと変位値を計算する：

二変量データのカーネル密度推定を行う：

推定された確率密度関数と累積分布関数を可視化する：

共分散と一般的なモーメントを計算する：

カーネル密度推定の記号表現を行う：

記号特性を調べる：

スコープ  (47)

基本的な用法  (8)

あるデータのカーネル密度推定を作る：

分布から確率を計算する：

単位付きの数量データについてのカーネル密度推定を作る：

モーメントを求める：

より滑らかな推定になるように帯域幅を広くする：

局所密度に従って適応的に帯域幅が変わるようにする：

データの特徴を検出して母数モデルフィットを補助する：

推定量は最大尤度推定の形と初期値の両方を示唆している：

より高次元でカーネ密度推定を使う：

四次元のカーネル密度推定：

分布からのサンプル：

カスタムカーネル関数を使ってカーネル密度推定の特性を探る：

多変量の推定に積タイプかラジアルタイプのカーネルを指定する：

分布特性  (10)

分布関数を推定する：

確率密度関数と累積分布関数の最初の数項：

分布のモーメントを計算する：

特殊なモーメント：

一般的なモーメント：

モーメントはしばしば閉形式で計算することができる：

記号による適応的帯域幅で分散について閉形式の式を計算する：

分位関数：

特殊な分位値：

乱数を生成する：

KernelMixtureDistributionと比較する：

確率と期待値を計算する：

母関数：

二変量分布関数を推定する：

二変量分布のモーメントを計算する：

特殊なモーメント：

一般的なモーメント：

乱数を生成する：

帯域幅の選択  (19)

使用する帯域幅を自動的に選ぶ：

データが多い程もとになっている分布がうまく近似できる：

帯域幅を明示的に指定する：

0.1と1.0の帯域幅を使う：

帯域幅が広い程滑らかな推定になる：

帯域幅が数値である必要はない：

推定値の確率密度関数と累積分布関数：

帯域幅を標準偏差の単位で指定する：

局所密度に従って適応的に帯域幅を変えられるようにする：

局所感度を0 (none)から1 (full)に変える：

感度をAutomaticに設定するとが使われる．ただし， はデータの次元である：

確率密度関数は等しい：

初期帯域幅を適応的推定に従って変える：

初期帯域幅をそれぞれ1と0.1に指定する：

いくつかの自動帯域幅選択法のうち任意のものを使う：

Silvermanのメソッドがデフォルトで使われる：

確率密度分布は等値である：

多変量の場合，帯域幅は正定値対称行列 × である：

スカラー h を与えると事実上 h IdentityMatrix[p]が使われる：

対角要素 d を指定すると事実上DiagonalMatrix[d]が使われる：

正定値対称行列である任意の × 行列を与えることができる：

デフォルトで各次元に別々に帯域幅を選ぶのにはSilvermanメソッドが使われる：

別々に対角の帯域幅要素を選ぶためには，どの自動メソッドを使ってもよい：

対角を推定するためのメソッドは同じではなくてもよい：

適応的帯域幅，過剰平滑化帯域幅，一定の帯域幅をそれぞれの次元に用いる：

一変量周辺分布の確率密度関数をプロットする：

すべての次元に同じ帯域幅を使うためにスカラー量を与える：

非零の対角から外れた要素を使うために，完全に指定された帯域幅行列を使う：

帯域幅行列は個々のカーネルの分散と方向を制御する：

スカラーの帯域幅：

次元ごとの帯域幅：

完全に指定された帯域幅行列：

いくつかの名前付き帯域幅メソッドは経験的アプローチに従っている：

いくつかの名前付き帯域幅メソッドの式：

推定は等しい：

最小二乗交差検定法：

ガウスカーネルと帯域幅 を使った確率密度関数の期待値：

一つ抜き交差確認法の密度推定値の確率密度関数の期待値：

帯域幅は に対する最小二乗交差確認関数を最小化することで求まる：

Sheather-Jones法はプラグイン推定器を使って帯域幅について解く：

Sheather-Jones推定器：

推定は等しい：

カーネル関数  (10)

いくつかのカーネル関数のうちから任意のものを指定する：

カーネル関数を純関数として定義する：

デフォルトでガウスカーネルが使われる：

これはNormalDistribution[0,1]の確率密度関数を使うことに等しい：

いくつかの一変量カーネル関数の形：

多変量データにいくつかのカーネル関数の中から任意のものを指定する：

いくつかの二変量積カーネルの形：

多変量データについて積タイプとラジアルタイプのカーネル関数のどちらかを選ぶ：

二次元の1つの双加重カーネルの計算：

ラジアル型：

帯域幅はラジアルタイプのカーネルと積タイプのカーネルの両方に同じような影響を与える：

スカラー帯域幅はカーネルを各次元に同じように引き伸ばす：

対角要素はカーネルを各軸に沿って別々に引き伸ばす：

非零の対角外要素は方向を変える：

さまざまなカーネル関数の確率密度関数：

正規分布に従うと仮定されるデータのもとでのカーネルの効率：

組込みのカーネル関数はすべて比較的に高い統計効率を有する：

オプション  (7)

MaxMixtureKernels  (7)

デフォルトで，カーネルはサンプル数300未満の各データ点に置かれている：

サンプルサイズが大きい場合はデフォルトで等間隔で置かれた最大で300個のカーネルが使われる：

推定に使うカーネルの最大数を指定する：

最高で5個のカーネルを置く：

カーネルの数が多い程もとになっている分布がうまく推定できる：

各データ点にカーネルを置く：

同数のカーネルで使われる帯域幅を変える：

二変量データについて各次元で使用されるカーネルの数を指定する：

それぞれ最高で10個と100個のカーネルを置く：

各次元に異なる最大カーネル数を設定する：

最大でそれぞれ5個と50個あるいは50個と5個のカーネルを指定する：

アプリケーション  (6)

推定密度を理論モデルと比較する：

高解像度が望ましい場合は適応的帯域幅と多くの混合カーネルを使う：

モデルのモーメントと推定は類似している：

NASDAQのApple株の日ごとの点変化の分布を推定する：

裾部が重いデータの場合は，より滑らかな推定を得るためにMaxMixtureKernelsオプションを大きくする：

指定された日に10%点以上変化する確率を計算する：

ニューヨーク州バッファローにおける降雪量を推定する：

帯域幅が違うと降雪分布が異なって表示される：

偽造紙幣を見分けるのに最も役に立つ測定法を6つの中から選ぶ：

測定法6が2種類の紙幣を見分けるのに最も適しているようである：

140.5mmで切り捨て，測定法6を分類器として使って，見分け損ないの確率を求める：

確率密度関数の平均二乗誤差を最小にする帯域幅を求める：

この帯域幅を使って確率密度関数を推定する：

KernelMixtureDistributionを使って楕円分布を作ることができる．楕円分布は多変量正規分布を一般化したものである：

周辺分布にNormalDistribution[0,1]を使うとMultinormalDistribution[μ,Σ]が与えられる：

他のいくつかの楕円分布：

特性と関係  (9)

結果の密度推定を積分すると1になる：

密度はカーネル関数の重み付き総和である：

KernelMixtureDistributionはもとになっている分布の一定推定器である：

実際に使われているカーネル数がサンプルサイズより大きいことはない：

最高で10000カーネル置く：

項数は使用されるカーネル数に一致する：

帯域幅が無限大に近付くにつれ，推定量がカーネルの形に近付く：

KernelMixtureDistributionの線形補間はSmoothKernelDistributionである：

KernelMixtureDistributionは結果としてカーネルのMixtureDistributionになる：

KernelMixtureDistributionは，入力がTimeSeriesあるいはEventSeriesのときにのみ，値に使うことができる：

以下と同じである：

KernelMixtureDistributionは，入力がTemporalDataのときは，すべての値に同時に働く：

以下と同じである：

考えられる問題  (5)

カーネル関数は確率密度関数である必要がある：

結果の密度推定は確率密度関数ではない：

自動適応帯域幅は大きいサンプルには小さすぎるかもしれない：

初期帯域幅を大きくする，MaxMixtureKernels，感度を下げる，等を試す：

記号データの場合，カーネルは各データ点に置かれなければならない：

MaxMixtureKernelsをAllかAutomaticに設定する：

記号データは"SheatherJones"と"LeastSquaresCrossValidation"のメソッドでは使えない：

推定を必要としない帯域幅を指定する：

カーネル関数の中には境界がありプロットで除外部分が出ることがある：

ExclusionsオプションをNoneに設定することで大きいギャップができずプロットにかかる時間も短縮することができる：

おもしろい例題  (2)

KernelMixtureDistributionを使ってガウスぼかしを二値化画像に適用する：

完全に記号的な三変量密度推定を計算する：

Wolfram Research (2010), KernelMixtureDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/KernelMixtureDistribution.html （2016年に更新）.

テキスト

Wolfram Research (2010), KernelMixtureDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/KernelMixtureDistribution.html （2016年に更新）.

CMS

Wolfram Language. 2010. "KernelMixtureDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/KernelMixtureDistribution.html.

APA

Wolfram Language. (2010). KernelMixtureDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/KernelMixtureDistribution.html

BibTeX

@misc{reference.wolfram_2024_kernelmixturedistribution, author="Wolfram Research", title="{KernelMixtureDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/KernelMixtureDistribution.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_kernelmixturedistribution, organization={Wolfram Research}, title={KernelMixtureDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/KernelMixtureDistribution.html}, note=[Accessed: 14-November-2024 ]}