KernelMixtureDistribution[{x1,x2,…}]
represents a kernel mixture distribution based on the data values xi.
KernelMixtureDistribution[{{x1,y1,…},{x2,y2,…},…}]
represents a multivariate kernel mixture distribution based on data values {xi,yi,…}.
KernelMixtureDistribution[…,bw]
represents a kernel mixture distribution with bandwidth bw.
KernelMixtureDistribution[…,bw,ker]
represents a kernel mixture distribution with bandwidth bw and smoothing kernel ker.


KernelMixtureDistribution
KernelMixtureDistribution[{x1,x2,…}]
represents a kernel mixture distribution based on the data values xi.
KernelMixtureDistribution[{{x1,y1,…},{x2,y2,…},…}]
represents a multivariate kernel mixture distribution based on data values {xi,yi,…}.
KernelMixtureDistribution[…,bw]
represents a kernel mixture distribution with bandwidth bw.
KernelMixtureDistribution[…,bw,ker]
represents a kernel mixture distribution with bandwidth bw and smoothing kernel ker.
Details and Options



- KernelMixtureDistribution returns a DataDistribution object that can be used like any other probability distribution.
- The probability density function for KernelMixtureDistribution for a value
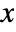 is given by
is given by 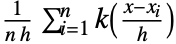 for a smoothing kernel
for a smoothing kernel 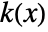 and bandwidth parameter
and bandwidth parameter 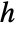 .
. - The following bandwidth specifications bw can be given:
-
h bandwidth to use {"Standardized",h} bandwidth in units of standard deviation {"Adaptive",h,s} adaptive bandwidth with initial bandwidth h and sensitivity s Automatic automatically computed bandwidth "name" use a named bandwidth selection method {bwx,bwy,…} separate bandwidth specifications for x, y, etc. - For multivariate densities, h can be a positive definite symmetric matrix.
- For adaptive bandwidths, the sensitivity s must be a real number between 0 and 1 or Automatic. If Automatic is used, s is set to
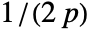 , where
, where 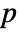 is the dimensionality of the data.
is the dimensionality of the data. - Possible named bandwidth selection methods include:
-
"LeastSquaresCrossValidation" uses the method of least-squares cross-validation "Oversmooth" 1.08 times wider than the standard Gaussian "Scott" uses Scott's rule to determine bandwidth "SheatherJones" uses the Sheather–Jones plugin estimator "Silverman" uses Silverman's rule to determine bandwidth "StandardDeviation" uses the standard deviation as bandwidth "StandardGaussian" optimal bandwidth for standard normal data - By default, the "Silverman" method is used.
- For automatic bandwidth computation, constant arrays are assumed to have unit variance.
- The following kernel specifications ker can be given:
-
"Biweight" 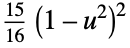
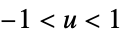
"Cosine" 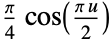
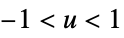
"Epanechnikov" 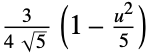
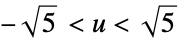
"Gaussian" 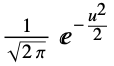
"Rectangular" 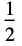
"SemiCircle" 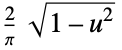
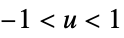
"Triangular" 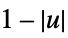
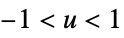
"Triweight" 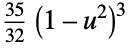
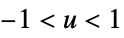
func 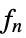
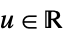
- In order for KernelMixtureDistribution to generate a true density estimate, the function fn should be a valid univariate probability density function.
- By default, the "Gaussian" kernel is used.
- For multivariate densities, the kernel function ker can be specified as product and radial types using {"Product",ker} and {"Radial",ker}, respectively. Product-type kernels are used if no type is specified.
- The precision used for density estimation is the minimum precision given in the bw and data.
- The following options can be given:
-
MaxMixtureKernels Automatic max number of kernels to use - KernelMixtureDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Examples
open all close allBasic Examples (3)
Create a kernel density estimate of univariate data:
Use the resulting distribution to perform analysis, including visualizing distribution functions:
Compute moments and quantiles:
Create a kernel density estimate of some bivariate data:
Visualize the estimated PDF and CDF:
Compute covariance and general moments:
Create symbolic representations of kernel density estimates:
Scope (47)
Basic Uses (8)
Create a kernel density estimate for some data:
Compute probabilities from the distribution:
Create a kernel density estimate for data with quantities:
Increase the bandwidth for smoother estimates:
Allow the bandwidth to vary adaptively with local density:
Identify features in data to aid in parametric model fitting:
The estimate suggests both the form and starting values for maximum likelihood estimation:
Use kernel density estimation in higher dimensions:
A four-dimensional kernel density estimate:
Explore properties of kernel density estimators using custom kernel functions:
Specify radial- or product-type kernels for multivariate estimates:
Distribution Properties (10)
Estimate distribution functions:
The first few terms of the PDF and CDF:
Compute moments of the distribution:
Moments can often be computed in closed form:
Compute a closed form expression for the variance with a symbolic adaptive bandwidth:
Compare with KernelMixtureDistribution:
Compute probabilities and expectations:
Estimate bivariate distribution functions:
Bandwidth Selection (19)
Automatically select the bandwidth to use:
More data yields better approximations to the underlying distribution:
Explicitly specify the bandwidth to use:
Use bandwidths of 0.1 and 1.0:
Larger bandwidths yield smoother estimates:
The bandwidth need not be numeric:
The PDF and CDF of the estimate:
Specify bandwidths in units of standard deviation:
Allow the bandwidth to vary adaptively with local density:
Vary the local sensitivity from 0 (none) to 1 (full):
Setting the sensitivity to Automatic uses ![]() where
where ![]() is the dimension of the data:
is the dimension of the data:
Vary the initial bandwidth for an adaptive estimate:
Specify an initial bandwidth of 1 and 0.1, respectively:
Use any of several automatic bandwidth selection methods:
Silverman's method is used by default:
In the multivariate case, the bandwidth is a symmetric positive definite ![]() ×
×![]() matrix:
matrix:
Giving a scalar h effectively uses h IdentityMatrix[p]:
Specifying diagonal elements d effectively uses DiagonalMatrix[d]:
Any ![]() ×
×![]() matrix that could be symmetric positive definite can be given:
matrix that could be symmetric positive definite can be given:
By default, Silverman's method is used to independently select bandwidths in each dimension:
Any automated method can be used to independently select diagonal bandwidth elements:
Methods used to estimate the diagonal need not be the same:
Use adaptive, oversmoothed, and constant bandwidths in the respective dimensions:
Plot the univariate marginal PDFs:
Give a scalar value to use the same bandwidth in all dimensions:
To use nonzero off-diagonal elements, give a fully specified bandwidth matrix:
The bandwidth matrix controls the variance and orientation of individual kernels:
Fully specified bandwidth matrices:
Some named bandwidth methods follow a rule-of-thumb approach:
Formulas for some named bandwidth methods:
The method of least-squares cross-validation:
The expectation of the PDF using a Gaussian kernel and bandwidth ![]() :
:
The expectation of the PDF of the leave-one-out density estimator:
The bandwidth is found by minimizing the least-squares cross-validation function over ![]() :
:
The method of Sheather and Jones uses a plugin estimator to solve for the bandwidth:
Kernel Functions (10)
Specify any one of several kernel functions:
Define the kernel function as a pure function:
By default, the Gaussian kernel is used:
This is equivalent to using the PDF of a NormalDistribution[0,1]:
Shapes of some univariate kernel functions:
Specify any one of several kernel functions for multivariate data:
Shapes of some bivariate product kernels:
Choose between product- and radial-type kernel functions for multivariate data:
Computation of a single biweight kernel in two dimensions:
Bandwidths have similar effects for both radial- and product-type kernels:
Scalar bandwidths stretch the kernel equally in each dimension:
Diagonal elements stretch the kernel independently along each axis:
Nonzero off-diagonal elements change the orientation:
The PDFs of the various kernel functions:
The efficiency of kernels under the assumption of normally distributed data:
The built-in kernel functions all have relatively high statistical efficiency:
Options (7)
MaxMixtureKernels (7)
By default, a kernel is placed at each data point for sample sizes less than 300:
For larger sample sizes, a maximum of 300 uniformly spaced kernels is used by default:
Specify the maximum number of kernels to use in the estimate:
A larger number of kernels gives a better estimate of the underlying distribution:
Place a kernel at each data point:
Vary the bandwidth used for the same number of kernels:
Specify the number of kernels to use in each dimension for bivariate data:
Place at most 10 and 100 kernels, respectively:
Set a different maximum number of kernels in each dimension:
Applications (6)
Compare an estimated density to a theoretical model:
Use an adaptive bandwidth and many mixture kernels when high resolution is desired:
The moments for the model and the estimate are similar:
Estimate the distribution of daily point changes for Apple stocks on the NASDAQ:
Increase the MaxMixtureKernels option with heavy-tailed data for a smoother estimate:
Compute the probability of a 10% point change or more on a given day:
Estimate the distribution of snowfall in Buffalo, New York:
Different bandwidths yield different descriptions of the snowfall distribution:
Identify which of six measures might be most useful for identifying counterfeit bank notes:
Measure 6 appears to best separate the two classes of notes:
Using measure 6 as a classifier with a cutoff of 140.5 mm, find the probability of misclassification:
Find the bandwidth that minimizes the mean squared error (MSE) of the PDF:
Use the bandwidth to estimate the PDF:
KernelMixtureDistribution can be used to create an elliptical distribution. Elliptical distributions are a generalization of multivariate normal distributions:
Using NormalDistribution[0,1] for the marginal gives MultinormalDistribution[μ,Σ]:
Properties & Relations (9)
The resulting density estimate integrates to unity:
The density is a weighted sum of kernel functions:
KernelMixtureDistribution is a consistent estimator of the underlying distribution:
The number of kernels actually used will be no larger than the sample size:
Placing at most 10000 kernels:
The number of terms corresponds to the number of kernels used:
As the bandwidth approaches infinity, the estimate approaches the shape of the kernel:
A linear interpolation of KernelMixtureDistribution is SmoothKernelDistribution:
KernelMixtureDistribution results in a MixtureDistribution of kernels:
KernelMixtureDistribution works with the values only when the input is a TimeSeries or an EventSeries:
KernelMixtureDistribution works with all the values together when the input is a TemporalData:
Possible Issues (5)
The kernel function needs to be a PDF:
The resulting density estimate is not a PDF:
Automatic adaptive bandwidths may be too small with large samples:
Try increasing the initial bandwidth, MaxMixtureKernels, or decreasing the sensitivity:
A kernel must be placed at each data point with symbolic data:
Set MaxMixtureKernels to All or Automatic:
Symbolic data cannot be used with the "SheatherJones" and "LeastSquaresCrossValidation" methods:
Specify bandwidths that do not require estimation:
Some of the kernel functions are bounded and trigger exclusions in plots:
Set the Exclusions option to None to avoid spurious gaps and to decrease plot timings:
Neat Examples (2)
Use KernelMixtureDistribution to apply a Gaussian blur to a binarized image:
Related Guides
Text
Wolfram Research (2010), KernelMixtureDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/KernelMixtureDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "KernelMixtureDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/KernelMixtureDistribution.html.
APA
Wolfram Language. (2010). KernelMixtureDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/KernelMixtureDistribution.html
BibTeX
@misc{reference.wolfram_2025_kernelmixturedistribution, author="Wolfram Research", title="{KernelMixtureDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/KernelMixtureDistribution.html}", note=[Accessed: 02-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_kernelmixturedistribution, organization={Wolfram Research}, title={KernelMixtureDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/KernelMixtureDistribution.html}, note=[Accessed: 02-February-2026]}